Решите два этих задания с решением.
​

Пошаговое объяснение:

2) Видимо, в задании опечатка и за исходную функцию берется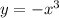 , а не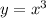

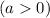смещение графика функции на единиц вниз показывает формула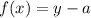

Значит, смещение графика функции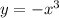 на 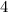единицы вниз показывает формула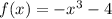

ответ: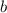  

3)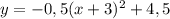 -квадратичная функция, ее график парабола, так как 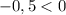, то ветви параболы направлены вниз, тогда функция возрастает на промежутке , где 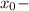абсцисса вершины параболы

Функция задана виде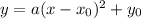 , значит, и промежуток возрастания функции

ответ: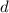  

2. а) Нет. здесь вправо на 4;

b)Да, здесь вниз на 4

c) Нет, здесь вверх на 4

d)Нет. здесь влево на 4

ответ b) f(x)=-x³-4

3. Графиком этой квадратичной функции служит парабола, ветви которой направлены вниз, т.к. первый коэффициент отрицат., он равен -0.5, вершина в точке (-3;4.5), поэтому промежуток возрастания d) (-∞;-3]

найдем производную. -х-3=0, х=-3- критческая точка

-3

   +                   -

ответ тот же . d)(-∞;-3]