Второе уравнение фактически получили такое же, как и было задано . Подобрать корни без решения уравнения через дискриминант в этом случае сложно . Поэтому реально работают первые два решения .
P.S. Легко подобрать корни по теореме Виета , например, для такого уравнения .
4) Графический решения уравнения . Построить параболу и найти точки пересечения с осью ОХ . Но в данном случае точные значения найти практически невозможно. Только приближённые значения : .
Такие квадратные уравнения, как это, можно решить, дополнив их до полного квадрата. Чтобы можно было дополнить уравнение до полного квадрата, оно должно иметь вид x²
+bx=c.
Делим обе части на −1.
Деление на −1 аннулирует операцию умножения на −1.
Делим −10, коэффициент члена x, на 2, в результате чего получится −5. Затем добавьте квадрат −5 в обе части уравнения. Это действие сделает левую часть уравнения полным квадратом.
1) Решение через дискриминант .
2) Решение с выделения полного квадрата .
3) Решение с теоремы Виета.
Второе уравнение фактически получили такое же, как и было задано . Подобрать корни без решения уравнения через дискриминант в этом случае сложно . Поэтому реально работают первые два решения .
P.S. Легко подобрать корни по теореме Виета , например, для такого уравнения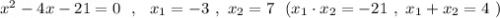 .
.
4) Графический решения уравнения . Построить параболу и найти точки пересечения с осью ОХ . Но в данном случае точные значения найти практически невозможно. Только приближённые значения :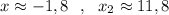 .
.
Такие квадратные уравнения, как это, можно решить, дополнив их до полного квадрата. Чтобы можно было дополнить уравнение до полного квадрата, оно должно иметь вид x²
+bx=c.
Делим обе части на −1.
Деление на −1 аннулирует операцию умножения на −1.
Делим −10, коэффициент члена x, на 2, в результате чего получится −5. Затем добавьте квадрат −5 в обе части уравнения. Это действие сделает левую часть уравнения полным квадратом.
Упрощаем:
Пошаговое объяснение: