Куб распилили на 64 одинаковых кубика. Так как объем куба считается по формуле V = a³ = 64, значит, каждое ребро распилили на 4 части:
V = 4³ = 64
Тогда окрашенными с двух сторон окажутся по 2 не угловых кубика вдоль каждого ребра (на рисунке - зеленого цвета).
У куба 12 ребер : 4 верхних, 4 нижних и 4 боковых.
Тогда окрашенными с двух сторон окажутся 2*12 = 24 кубика.
Итак, нужных кубиков - 24.
Всего - 64
Вероятность, что первый вытянутый с двумя окрашенными гранями :
p₁ = 24/64 = 3/8
Вероятность, что второй вытянутый с двумя окрашенными гранями :
p₂ = 23/63
Вероятность, что оба кубика нужные
p = p₁*p₂ =
по формулам
Благоприятные события - сочетание 2 кубиков из 24 без повторений
Все события - сочетание 2 кубиков из 64 без повторений
Вероятность
ответ: р= ≈ 0,137
Куб распилили на 64 одинаковых кубика. Так как объем куба считается по формуле V = a³ = 64, значит, каждое ребро распилили на 4 части:
V = 4³ = 64
Тогда окрашенными с двух сторон окажутся по 2 не угловых кубика вдоль каждого ребра (на рисунке - зеленого цвета).
У куба 12 ребер : 4 верхних, 4 нижних и 4 боковых.
Тогда окрашенными с двух сторон окажутся 2*12 = 24 кубика.
Итак, нужных кубиков - 24.
Всего - 64
Вероятность, что первый вытянутый с двумя окрашенными гранями :
p₁ = 24/64 = 3/8
Вероятность, что второй вытянутый с двумя окрашенными гранями :
p₂ = 23/63
Вероятность, что оба кубика нужные
p = p₁*p₂ =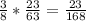
по формулам
Благоприятные события - сочетание 2 кубиков из 24 без повторений
Все события - сочетание 2 кубиков из 64 без повторений
Вероятность
ответ: р=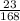 ≈ 0,137
≈ 0,137
Чтобы ученик сдал зачет 2ой раз, надо, чтобы 1ый раз он провалил, поэтому найдем вероятность провала 1ого зачета:
Вер. = 10/25 = 0.4 (10 вопросов, на которые он не знает ответ, 25 вопросов - всего)
Сответственно, только если 0.4 "случится", ученик пойдет сдавать экзамен 2ой раз, а значит вероятность в ответе к задаче будет уже меньше 0.4.
Теперь найдем вероятность успеха сдачи 2ого зачета:
Вер. = 15/25 = 0.6 (15 вопросов, на которые он знает ответ, 25 вопросов - всего)
Последний этап - перемножить вероятности:
0.4×0.6 = 0.24 (или 24%)
ответ: 0.24 (или 24%)