Скількома студент може одержати оцінки, не нижчі за 3, таким чином, щоб їх сума дорівнювала 30?

Это формула Бернулли. Если коротко: существует всего выбрать одно элементарное событие из 6^7 возможных, так, чтобы пятерка выпала только в двух испытаниях. Вероятность каждого из таких событий - это произведение вероятностей двукратного выпадения 5 и пятикратного выпадения не 5, то есть . Умножая на число событий, получаем, что вероятность искомого события равна , или приблизительно 23,44%

Формула Бернулли в общем виде: вероятность того, что из n независимых испытаний событие с вероятностью p ("успех") наступит ровно k раз, равна

1.

2.

a)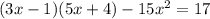  

     

     

     

     

     

b)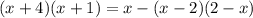    

     

     

     

     

     

3.     =

       

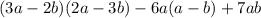 Чтобы найти значение выражения, надо знать

только значение переменной b.

ответ:        3) Только переменной b.

4.  

Пусть х - цифра десятков, тогда

         (12-х)  - цифра единиц

получаем

10х+(12-х)=  (9х+12) - данное  двузначное число.      

(12-х)*10+х= (120-9х) - обратное число к данному.

По условию: если к данному двузначному числу прибавить 54, то получится число, обратное данному.

Уравнение:

(9х+12) + 54 =  (120-9х)

9х+9х = 120 -12-54

    18х = 54

   х = 54 : 18

    х = 3 цифра десятков, тогда

 12 - 3 = 9  - цифра единиц.

39 - данное  двузначное число.

ответ:  39.