Математика: Сколько будет 200+300*500: 700-300*500

Сколько будет 200+300500: 700-300500

Показать ответ

Ответ:

Sunlight11

16.05.2022 10:15

Площадь трапеции равна 10√3 см².

Пошаговое объяснение:

Пусть дана прямоугольная трапеция ABCD , AD║BC , ∠ADC =30°,

AC =4 cм и диагональ АС перепендикулярна боковой стороне

AC ⊥ CD.

Так как диагональ АС перепендикулярна боковой стороне CD , то

Δ ACD - прямоугольный и ∠ADC =30°. По свойству катета, лежащего напротив угла в 30° , гипотенуза AD в 2 раза больше катета АС.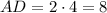 $AD =2\cdot4 =8$ см.

Воспользуемся теоремой Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Найдем боковую сторону трапеции, как катет прямоугольного треугольника Δ ACD .

$CD ^{2} =AD^{2} -AC ^{2} ;\\CD =\sqrt{AD^{2} -AC ^{2}} ;\\CD = \sqrt{8^{2} -4^{2} }=\sqrt{(8-4)(8+4)} =\sqrt{4\cdot12} =\sqrt{4\cdot4 \cdot3} =4\sqrt{3}$ см.

Найдем высоту прямоугольного треугольника СН , она является и высотой трапеции.

Для того чтобы найти высоту прямоугольного треугольника, проведенную к гипотенузе, надо произведение катетов разделить на гипотенузу .

$CH = \dfrac{AC \cdot CD }{AD} ;CH = \dfrac{4 \cdot 4\sqrt{3} }{8}=\dfrac{16\sqrt{3} }{8} =2\sqrt{3}$ см .

Или СН - это в Δ СНD катет, лежащий напротив угла в 30 ° и

$CH= \dfrac{1}{2} CD ;\\CH= \dfrac{1}{2} \cdot4\sqrt{3} =2\sqrt{3}$ см.

Рассмотрим Δ АВС - прямоугольный, АВ = СН =2√3 см. Найдем катет ВС по теореме Пифагора .

$BC ^{2} =AC^{2} -AB ^{2} ;\\BC= \sqrt{AC^{2} -AB ^{2} } ;\\BC= \sqrt{4^{2}-(2\sqrt{3)^{2} } } =\sqrt{16-12} =\sqrt{4} =2$

Найдем площадь трапеции как произведение полусуммы оснований на высоту трапеции.

$S=\dfrac{BC+AD}{2} \cdot CH;S=\dfrac{2+8}{2} \cdot 2\sqrt{3} =5\cdot2\sqrt{3} =10\sqrt{3}$

Площадь трапеции равна 10√3 см².

#SPJ1

Буду благодарен если дана прямоугольная трапеция abcd в которой ad параллельно bc, угол abc = 90 гра

0,0(0 оценок)

Ответ:

Tapoocek

15.01.2023 02:13

$z = {x}^{ \sqrt{y} } ln(y + x) \\ z'_{x} = \sqrt{y} {x}^{ \sqrt{y} - 1 } ln(y + x) + {x}^{ \sqrt{y} } \frac{1}{y + x} \\ z'_{y} = {x}^{ \sqrt{y} } lnx \frac{1}{2 \sqrt{y} } ln(y + x) + {x}^{ \sqrt{y} } \frac{1}{y + x}$

$z = \frac{ {cosy}^{2} }{x} \\ z'_{x} = - \frac{ {cosy}^{2} }{ {x}^{2} } \\ z'_{y} = \frac{ - 2y {siny}^{2} }{x}$

Пошаговое объяснение:

похідні по х і у першої функції це похідна добутку, щоб знайти таку похідну треба знайти суму: друга функція помножити на похідну першої функції плюс перша функція помножити на похідну другої функції

спочатку знайдемо похідну z по х значить у тут в ролі сталої, тобто шукаємо як похідну хⁿ і дописуємо другу функцію з логарифмом, потім шукаємо похідну від логарифма і дописуємо х^√у,

якщо z' по у, то тут х в ролі сталої, шукаємо похідну (а^х)'=а^хlnа і оскільки тут √у то ще треба записати похідну від кореня і дописати ln(y+x) і другий додаток такий же як в похідні по х

похідна по х і у другої функції це звичайна похідна в першому випадку це (1/х)'=-1/х² але замість одиниці записуємо cosy², в другому випадку треба знайти похідну (cosy²)'=-siny²×(у²)'=-2уsiny² і дописати 1/х як сталу

0,0(0 оценок)

Популярные вопросы: Математика