Скорость катера по течению реки равна 24,4 км/ч, а собственная скорость катера – 2,9 км/ч. Найдите собственную скорость баржи и ее скорость против течения
Пусть p нечетно, то есть p отлично от двух, тогда p и p+2 - взаимнопростые.
У простого числа p два делителя: p и 1, тогда поскольку 1 единственный общий делитель с p+2 или (p+2)^2, то если (p+2)^2 имеет n делителей:
d1=1,d2,d3,...,dn = (p+2)^2, то число p(p+2)^2 имеет делители:
d1=1, d2, d3,..., dn = (p+2)^2, pd1=p, pd2, pd3,..., pdn = p(p+2)^2 - имеет 2n делителей, тогда (p+2)^2 имеет ровно 30/2 = 15 делителей.
Пусть: p1, p2, p3,..., pk - простые делители числа (p+2)^2 в произвольном порядке, а поскольку (p+2)^2 - полный квадрат, то каждое простое число из множества p1, p2, p3,..., pk встречаются четное число раз в разложении числа (p+2)^2 на простые множители.
Пусть каждое из чисел p1, p2, p3,..., pk встречается :
2n1, 2n2, 2n3,..., 2nk раз cоответственно, тогда из комбинаторных соображений общее число делителей числа (p+2)^2 равно: (у числа p+2 они встречаются n1,n2,n3,..., nk раз)
(2n1 + 1)(2n2+1)(2n3 + 1)...(2nk + 1) = 15 = 5*3
5*3 имеет 4 положительных делителя: 1,3,5,15. 1 не подходит, ибо 2ni + 1 >=3
То есть имеем два варианта. У числа (p+2)^2 только 2 простых делителя, каждый из которых встречается n1 и n2 раза:
2n1 + 1 = 3
n1 = 1
2n2 + 1 = 5
n2 = 2
Иначе говоря:
p+2 = p1*p2^2
Или второй вариант:
у числа (p+2) один простой делитель, что встречается n1 раз :
Воспользуемся методом, позволяющим находить в разложении многочлена на скобки выражения вида Если a>0, это сразу дает два решения если a<0, действительные корни эта скобка не дает, но по любому степень многочлена будет понижена на 2. Кстати, решения вида я называю парными; название мне кажется оправданным. Легко доказать, что многочлен P(x) имеет парные корни тогда и только тогда, когда они обращают в ноль по отдельности сумму четных степеней и сумму нечетных степеней. Это следует из того, что сумма четных степеней равна а сумма нечетных равна
Кстати, это утверждение будет работать и для нулевого корня, если считать, что ноль является парным корнем, в том случае, когда он является кратным.
1) Разбиваем на четные и нечетные степени:
найденные t удовлетворяют и первому уравнению, поэтому оно принимает вид (t-2)(t+1)(t+3)=0, а поскольку исходное уравнение может быть получено в виде суммы этих двух, получаем
ответ: 43
Пошаговое объяснение:
p^3 + 4p^2 + 4p = p(p+2)^2
Пусть p нечетно, то есть p отлично от двух, тогда p и p+2 - взаимнопростые.
У простого числа p два делителя: p и 1, тогда поскольку 1 единственный общий делитель с p+2 или (p+2)^2, то если (p+2)^2 имеет n делителей:
d1=1,d2,d3,...,dn = (p+2)^2, то число p(p+2)^2 имеет делители:
d1=1, d2, d3,..., dn = (p+2)^2, pd1=p, pd2, pd3,..., pdn = p(p+2)^2 - имеет 2n делителей, тогда (p+2)^2 имеет ровно 30/2 = 15 делителей.
Пусть: p1, p2, p3,..., pk - простые делители числа (p+2)^2 в произвольном порядке, а поскольку (p+2)^2 - полный квадрат, то каждое простое число из множества p1, p2, p3,..., pk встречаются четное число раз в разложении числа (p+2)^2 на простые множители.
Пусть каждое из чисел p1, p2, p3,..., pk встречается :
2n1, 2n2, 2n3,..., 2nk раз cоответственно, тогда из комбинаторных соображений общее число делителей числа (p+2)^2 равно: (у числа p+2 они встречаются n1,n2,n3,..., nk раз)
(2n1 + 1)(2n2+1)(2n3 + 1)...(2nk + 1) = 15 = 5*3
5*3 имеет 4 положительных делителя: 1,3,5,15. 1 не подходит, ибо 2ni + 1 >=3
То есть имеем два варианта. У числа (p+2)^2 только 2 простых делителя, каждый из которых встречается n1 и n2 раза:
2n1 + 1 = 3
n1 = 1
2n2 + 1 = 5
n2 = 2
Иначе говоря:
p+2 = p1*p2^2
Или второй вариант:
у числа (p+2) один простой делитель, что встречается n1 раз :
2n1 +1 = 15
n1 = 7
p+2 = p1^7
Рассмотрим первый случай:
p+2 = p1*p2^2
p = p1*p2^2 - 2
Минимально возможные нечетные p1 и p2: p1 = 3; p2 = 5.
Нетрудно заметить, что 5*3^2 - 2 = 43 - простое, а значит
p = 5*3^2 - 2 = 43 - минимальное нечетное простое число удовлетворяющее условию при данном варианте.
Второй случай рассматривать нет смысла, ибо :
p = p1^7 - 2 >= 3^7 - 2 > 43
Осталось проверить тривиальный случай p = 2
p(p+2)^2 = 2*4^2 = 2^5 - имеет 6 делителей.
Таким образом, наименьшее простое число p такое, что p^3+4p^2+4p имеет ровно 30 положительных делителей это 43.
Воспользуемся методом, позволяющим находить в разложении многочлена на скобки выражения вида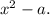 Если a>0, это сразу дает два решения
Если a>0, это сразу дает два решения 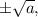 если a<0, действительные корни эта скобка не дает, но по любому степень многочлена будет понижена на 2. Кстати, решения вида
если a<0, действительные корни эта скобка не дает, но по любому степень многочлена будет понижена на 2. Кстати, решения вида 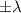 я называю парными; название мне кажется оправданным. Легко доказать, что многочлен P(x) имеет парные корни
я называю парными; название мне кажется оправданным. Легко доказать, что многочлен P(x) имеет парные корни 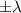 тогда и только тогда, когда они обращают в ноль по отдельности сумму четных степеней и сумму нечетных степеней. Это следует из того, что сумма четных степеней равна
тогда и только тогда, когда они обращают в ноль по отдельности сумму четных степеней и сумму нечетных степеней. Это следует из того, что сумма четных степеней равна 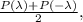 а сумма нечетных равна
а сумма нечетных равна 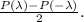
Кстати, это утверждение будет работать и для нулевого корня, если считать, что ноль является парным корнем, в том случае, когда он является кратным.
1) Разбиваем на четные и нечетные степени: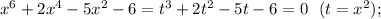
найденные t удовлетворяют и первому уравнению, поэтому оно принимает вид (t-2)(t+1)(t+3)=0, а поскольку исходное уравнение может быть получено в виде суммы этих двух, получаем
(t-2)(t+1)(t+3)-2x(t-2)(t+1)=0; (t-2)(t+1)(t-2x+3)=0; (x²-2)(x²+1)(x²-2x+3)=0.
ответ:
2) t³+6t²+11t+6=0; -2x(t^2+3t+2)=-2x(t+1)(t+2)=0;
t³+6t²+11t+6=(t+1)(t+2)(t+3); все уравнение принимает вид
(t+1)(t+2)(t+3)-2x(t+1)(t+2)=(t+1)(t+2)(t-2x+3)=(x²+1)(x²+2)(x²-2x+3)=0.
ответ: решений нет.