Составьте уравнение касательной к графику функции f(x) = √(x² - 3), проходящей через точку А(1;-1)
Пошаговое объяснение:
Пусть х₀-точка касания графика и прямой. Уравнение касательной
y = f ’(x₀) • (x − x₀) + f (x₀) .
f (x₀) =√(x₀² - 3),
f ’(x)= , f ’(x₀)=
y = * (x − x₀) + √(x₀² - 3) . Точка А(1;-1) принадлежит этой касательной , значит ее координаты удовлетворяют этому уравнению
-1 = * (1 − x₀) + √(x₀² - 3)
-1*√(x²₀-3) =x₀(1-x₀)+(x₀²-3)
-1*√(x²₀-3) =x₀-x₀²+x₀²-3 , -1*√(x²₀-3) =x₀ -3 , 3- x₀ =√(x²₀-3),
(3- x₀)² =x²₀-3 , 9-6x₀ +x₀²= x²₀-3 , x₀=2
Тогда f ’(2)= , f (2) =√(2² - 3) =1.
y = 2 • (x − 2) +1 или у=2х-3 .
Составьте уравнение касательной к графику функции f(x) = √(x² - 3), проходящей через точку А(1;-1)
Пошаговое объяснение:
Пусть х₀-точка касания графика и прямой. Уравнение касательной
y = f ’(x₀) • (x − x₀) + f (x₀) .
f (x₀) =√(x₀² - 3),
f ’(x)=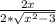 , f ’(x₀)=
, f ’(x₀)= 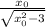
y =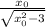 * (x − x₀) + √(x₀² - 3) . Точка А(1;-1) принадлежит этой касательной , значит ее координаты удовлетворяют этому уравнению
* (x − x₀) + √(x₀² - 3) . Точка А(1;-1) принадлежит этой касательной , значит ее координаты удовлетворяют этому уравнению
-1 =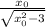 * (1 − x₀) + √(x₀² - 3)
* (1 − x₀) + √(x₀² - 3)
-1*√(x²₀-3) =x₀(1-x₀)+(x₀²-3)
-1*√(x²₀-3) =x₀-x₀²+x₀²-3 , -1*√(x²₀-3) =x₀ -3 , 3- x₀ =√(x²₀-3),
(3- x₀)² =x²₀-3 , 9-6x₀ +x₀²= x²₀-3 , x₀=2
Тогда f ’(2)=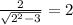 , f (2) =√(2² - 3) =1.
, f (2) =√(2² - 3) =1.
y = 2 • (x − 2) +1 или у=2х-3 .