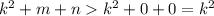Пусть, не нарушая общности,
Тогда
С другой стороны, т.к. числа натуральные,
- последовательные натуральные числа. По условию - полный квадрат. Тогда получается, что он "зажат" между квадратами двух последовательных натуральных чисел, что, очевидно, невозможно. Противоречие. А значит таких натуральных чисел не существует.
Пусть, не нарушая общности,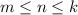
Тогда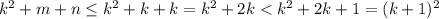
С другой стороны, т.к. числа натуральные,