Сын всемирно известного путешественника Валериан Фогг заключил пари, что сможет повторить кругосветное путешествие своего отца. В каждом городе, который он должен посетить, есть либо морской порт, либо аэропорт. Города можно задать как строку s длины n, где si = А, если в i-м городе есть аэропорт, и si=М, если в i-м городе есть морской порт. Сейчас Валериан находится в первом городе (которому соответствует s1), и ему нужно попасть в последний город (которому соответствует sn). Если для двух городов i и j на всех перекрестках i,i+1,…,j−1 есть морской порт, то можно заплатить a дублонов за билет на корабль, и доплыть от i-го города до j-го (в нем порт может и отсутствовать). Формально, заплатив a дублонов, Валериан может добраться из i до j, если st=М для всех i ≤ t < j. То же верно и для аэропортов, но цена билета на дирижабль равна b. Например, если s=«AAМММAМ», a=4 и b=3, то Валериан может: купить билет на дирижабль, чтобы добраться от 1 до 3, купить билет на корабль, чтобы добраться от 3 до 6, купить билет на дирижабль, чтобы добраться от 6 до 7. Так ему нужно потратить 4+3+4=11 дублонов. Обратите внимание, последний город (т.е. символ sn) не влияет на итоговую стоимость. Однако пари Валериан выиграет, только если сможет повторить подвиг отца, и наличных у него всего р, чего может не хватить на весь маршрут. Однако старый друг готов и доставить Валериана в любой город. Но что бы пари считалась выигранным необходимо, чтобы это был ближайший город i к первому так, чтобы ему хватило денег добраться от i-го города до n-го. Напишите программу, которая вычислит минимальный номер города i, до которого Валериана должен доставить друг. Формат ввода В первой строке входных данных даны три целых числа a,b,p — стоимость билета на дирижабль, стоимость билета на корабль, и количество денег у Валериана соответственно (1 ≤ a, b, p ≤105). Во второй строке входных данных дана строка s, в которой si=A, если в i-м городе можно сесть на дирижабль, и si=М, если в i-м городе можно сесть на корабль. (2 ≤ длина строки s ≤ 105). Формат вывода В выходные данные необходимо вывести одно целое число i — минимальный номер города , до которого Валериана должен доставить друг. Пример 1 Ввод Вывод 3 2 8 MM 2 Пример 2 Ввод Вывод 5 3 4 1 Пример 3 Ввод Вывод 2 1 1 AMAAAM 3
Правильная игра первого игрока - расставлять в одну строку наибольшие числа, правильная игра второго игрока - расставлять в одну строку меньшие числа.
При правильной игре обоих они будут расставлять числа в одну и ту же строку.
Тогда первый поставит в первую строку числа 64, 63, 62 и 61, второй - числа 1, 2, 3 и 4. Сумма чисел в строке будет 260.
Во вторую строку первый поставит числа 60, 59, 58 и 57, второй - 5, 6, 7 и 8. Сумма чисел в строке будет 260.
И так далее. Сумма чисел в каждой строке будет равна 260.
5) х= -1
6) 30
7) -8,1
8) 1839,12792
9) у₁=0,2
у₂= -1,4
Пошаговое объяснение:
5) -2*(Х-2)+3(2-3Х)=21
-2х+4+6-9х=21
-11х=21-4-6
-11х=11
х= -1
6) -0,25*2/3*(-40)*(4,5)=45*2/3=30
7) (-3,25-(-1,75)):(0,6)+0,8*(-7)= -2,5-5,6= -8,1
8) 1.у=4,520-5\8(3,2а-13/5в)-7,2(-4,9а+2,5в) якщо а=-10;в=0,1
у=4,520-5\8(3,2а-13/5в)-7,2(-4,9а+2,5в)
у=4,520-2а+1,625в+35,28а-18в
у=4,520+33,28*(-10)-16,275*0,1
у=4,520-332,8-1,6375
у= -329,9157
2. 0,5*(1,6Х-6,4у)-2,4(1,5Х+у) якщоХ=3; у= -329,9157
0,5*(1,6Х-6,4у)-2,4(1,5Х+у)= 0,8Х-3,2у-3,6Х-2,4у= -2,8*3-5,6*-329,9157= -8,4+1847,52792= 1839,12792
9) (5у+7)(2у-0,4)=0
10у^2-2у+14у-2,8=0
10у^2+12у-2,8=0
D=144-4*10*(-2,8)=144+112=256=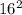
у₁=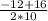
=
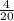=0,2
у₂=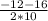
=
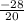= -1,4