11.
| : 5
x > 2
ответ: 3 (x∈(2 ; +∞))
12. lg² x - 3 lg x - 10 = 0
Пусть lg x = t, тогда
t² - 3t - 10 = 0
D = (-3)² - 4 * 1 * (-10) = 9 + 40 = 49 = 7²
5 * (-2) = -10
ответ: 2 ( -10)
13. 2 cos² x - 3 sin x = 0
cos² x = 1 - sin² x по основному тригонометрическому тождеству
2 * (1 - sin² x) - 3 sin x = 0
2 - 2 sin² x - 3 sin x = 0
- 2 sin² x - 3 sin x + 2 = 0 | : (-1)
2 sin² x + 3 sin x - 2 = 0
Пусть sin x = t, тогда
2 t² + 3t - 2 = 0
D = 3² - 4 * 2 * (-2) = 9 + 16 = 25 = 5²
- посторонний корень, т.к. в уравнении sin x = a, |a|≤1
Вернёмся к замене:
, m∈Z
ответ: 4 ( , m∈Z )
Пошаговое объяснение:
1 Задание.
Вспоминаем или узнаем одно из свойств корней:
, тогда в первом задании:
Теперь вспоминаем свойство степеней при делении:
, тогда выходит:
Вернем 4 на место
, мы можем вытащить степень за корень и получим:
возведение в отрицательную степень:
В нашем случае: . ответ: 3
2 Задание:
, Здесь используем формулу сокращенного умножения:
, сокращаем одну скобку и у нас остается
. ответ: 1) -5
3 Задание:
Ну что, вспоминаем формулы по логарифмам:
logb = c
Нам это подходит для последнего, где 5. То есть,
Вспоминаем или узнаем еще одну формулу:
В нашем случае:
, Мы знаем чтобы получить из 3 9, нужно возвести её во вторую степень, поэтому так и выходит. Теперь все соединяем и получаем:
. ответ 3) 4
Ну вот и все объяснения
11.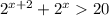
x > 2
ответ: 3 (x∈(2 ; +∞))
12. lg² x - 3 lg x - 10 = 0
Пусть lg x = t, тогда
t² - 3t - 10 = 0
D = (-3)² - 4 * 1 * (-10) = 9 + 40 = 49 = 7²
5 * (-2) = -10
ответ: 2 ( -10)
13. 2 cos² x - 3 sin x = 0
cos² x = 1 - sin² x по основному тригонометрическому тождеству
2 * (1 - sin² x) - 3 sin x = 0
2 - 2 sin² x - 3 sin x = 0
- 2 sin² x - 3 sin x + 2 = 0 | : (-1)
2 sin² x + 3 sin x - 2 = 0
Пусть sin x = t, тогда
2 t² + 3t - 2 = 0
D = 3² - 4 * 2 * (-2) = 9 + 16 = 25 = 5²
Вернёмся к замене:
ответ: 4 (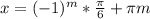 , m∈Z )
, m∈Z )
Пошаговое объяснение:
1 Задание.
Вспоминаем или узнаем одно из свойств корней:
Теперь вспоминаем свойство степеней при делении:
Вернем 4 на место
возведение в отрицательную степень: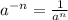
В нашем случае:![(\sqrt[4]{a}) ^ {-1} = \frac{1}{\sqrt[4]{a} }](/tpl/images/1344/5744/b0179.png) . ответ: 3
. ответ: 3
2 Задание:
3 Задание:
Ну что, вспоминаем формулы по логарифмам:
log b = c
b = c
Нам это подходит для последнего, где 5. То есть,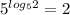
Вспоминаем или узнаем еще одну формулу:
В нашем случае:
Ну вот и все объяснения