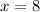теплохід ішов 4.5 год проти течії річки і 0.8 - за течією і пройшов 142,8 км знайдіть власну швидкість теплохода (у км/год) якщо швидкість течії дорівнює 1.8 км/год
построить равнобедренный треугольник с двумя сторонами 3см и 6 см...
должна быть еще одна сторона. Если попробовать взять 3 см,то построить треугольник не удастся. Почему? Да просто сумма двух сторон ВСЕГДА больше третьей стороны! А 3+3=6. Знапчит 3 не годится. Если взять 6,то вполне возможно. Как сделать построение? Взять отрезок 3м. и из его концов описать окружности раджиусом 6см. точки пересечения окружностей и дадут искомую третью вершину. Две стороны= радиусам по 6 см и основание равное 3 см.Получится два треугольника,один сверху основания ,а другой снизу. Абсолютно одинаковые треугольники , симметричные основанию.
По определению логарифма заметим, что основание (a) всегда должно быть больше "0" и не равное "1". Число "b" всегда строго положительное, т.к. при возведение любого положительного числа "а" в любую степень "с", мы получим строго положительное значение.
Рассмотрим наше уравнение:
ОДЗ (область допустимых значений):
Используем потенцирования, т.е. отбросим часть с логарифмом (мы имеем на это право, т.к. основание у логарифмов одинаковые и никаких посторонних членов нет)
Пошаговое объяснение:
построить равнобедренный треугольник с двумя сторонами 3см и 6 см...
должна быть еще одна сторона. Если попробовать взять 3 см,то построить треугольник не удастся. Почему? Да просто сумма двух сторон ВСЕГДА больше третьей стороны! А 3+3=6. Знапчит 3 не годится. Если взять 6,то вполне возможно. Как сделать построение? Взять отрезок 3м. и из его концов описать окружности раджиусом 6см. точки пересечения окружностей и дадут искомую третью вершину. Две стороны= радиусам по 6 см и основание равное 3 см.Получится два треугольника,один сверху основания ,а другой снизу. Абсолютно одинаковые треугольники , симметричные основанию.
По определению логарифма заметим, что основание (a) всегда должно быть больше "0" и не равное "1". Число "b" всегда строго положительное, т.к. при возведение любого положительного числа "а" в любую степень "с", мы получим строго положительное значение.
Рассмотрим наше уравнение:
Используем потенцирования, т.е. отбросим часть с логарифмом (мы имеем на это право, т.к. основание у логарифмов одинаковые и никаких посторонних членов нет)
Запишем ответ:
ответ: