Пошаговое объяснение:
а) разделил на 2 интеграла по разности, под первым e^(pi) - константа, поэтому получится e^(pi) * x = pi* e^(pi) - 0 ( при подстановке)
второй - табличный = sinx + C = 0 в подстановке.
ответ: pi* e^(pi)
б) занесу cosx под дифференциал
cosxdx = d ( sinx + 1)
дальше простой степенной интеграл = 1/3*(1+sinx)^3 + C = 1/3 * (1)^3 - 1/3 * (1)^3 = 0
в) опять под дифференциал
d(4-t^2) = -2*t dt => tdt = -1/2 * d(4-t^2)
дальше простой степенной интеграл = -1/2*2*(4-t)^(1/2) + C = -3^(1/2) + 4^(1/2) = 2 -
г) под дифференциал:
d(1 + 4x^3) = 12x^2 dx => 6x^2dx = 1/2 d(1+4x^3)
дальше табличный интеграл = 1/2 * ln(1+4x^3) + C = 1/2*ln5 - 1/2*ln1 = 1/2*ln5
Дан квадрат
1. Выполни параллельный перенос квадрата на вектор →.
2. Каким образом ещё можно получить тот же результат?
1)Поворотом на 180 градусов вокруг конечной точки данного вектора
2)Поворотом на 180 градусов вокруг начальной точки данного вектора
3)Выполненный параллельный перенос на данный вектор — единственное возможное движение
4)Параллельным переносом на противоположный вектор
5)Симметрией относительно конечной точки данного вектора
6)Симметрией относительно прямой, на которой лежит данный вектор
7)Поворотом на −180 градусов вокруг конечной точки данного вектора
Пошаговое объяснение:
а) разделил на 2 интеграла по разности, под первым e^(pi) - константа, поэтому получится e^(pi) * x = pi* e^(pi) - 0 ( при подстановке)
второй - табличный = sinx + C = 0 в подстановке.
ответ: pi* e^(pi)
б) занесу cosx под дифференциал
cosxdx = d ( sinx + 1)
дальше простой степенной интеграл = 1/3*(1+sinx)^3 + C = 1/3 * (1)^3 - 1/3 * (1)^3 = 0
в) опять под дифференциал
d(4-t^2) = -2*t dt => tdt = -1/2 * d(4-t^2)
дальше простой степенной интеграл = -1/2*2*(4-t)^(1/2) + C = -3^(1/2) + 4^(1/2) = 2 -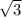
г) под дифференциал:
d(1 + 4x^3) = 12x^2 dx => 6x^2dx = 1/2 d(1+4x^3)
дальше табличный интеграл = 1/2 * ln(1+4x^3) + C = 1/2*ln5 - 1/2*ln1 = 1/2*ln5
Дан квадрат
1. Выполни параллельный перенос квадрата на вектор →.
2. Каким образом ещё можно получить тот же результат?
1)Поворотом на 180 градусов вокруг конечной точки данного вектора
2)Поворотом на 180 градусов вокруг начальной точки данного вектора
3)Выполненный параллельный перенос на данный вектор — единственное возможное движение
4)Параллельным переносом на противоположный вектор
5)Симметрией относительно конечной точки данного вектора
6)Симметрией относительно прямой, на которой лежит данный вектор
7)Поворотом на −180 градусов вокруг конечной точки данного вектора