Пошаговое объяснение:SKLR является параллелограммом Тогда KL= SR ⇒ KL= SH+HR = 7,7 +12,5 =20,2
После проведения высоты KH выходит ; что ∠SHQ = ∠QKL =90 ; и так как ∠SQH , ∠KQL являются вертикальными углами то ∠SQH = ∠KQL Из чего исходя ΔSQH ≅ ΔQKL , раз они подобны можно вывести что
Пошаговое объяснение:
SKLR является параллелограммом
Тогда
KL= SR ⇒ KL= SH+HR = 7,7 +12,5 =20,2
После проведения высоты KH выходит ; что ∠SHQ = ∠QKL =90 ; и так как ∠SQH , ∠KQL являются
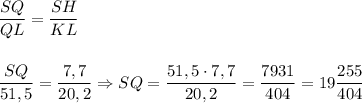
вертикальными углами то ∠SQH = ∠KQL
Из чего исходя ΔSQH ≅ ΔQKL , раз они подобны можно вывести что
Для решения этой задачи нам понадобятся знания о параллелограммах, диагоналях, высотах и их свойствах.
Давайте проанализируем параллелограмм SKLR и данную информацию:
- Мы знаем, что SH = 7,7 см.
Давайте обозначим точку пересечения Q как (x, y), где x - SQ, y - QL.
- Мы также знаем, что HR = 12,5 см и QL = 51,5 см.
Сначала рассмотрим треугольник SQH. У него сторона SQ будет равна x, высота SH равна 7,7 см, а сторона QH - нужно вычислить.
Мы можем использовать теорему Пифагора, чтобы найти значения сторон SQH: SQ^2 + QH^2 = SH^2
Теперь подставим известные значения:
x^2 + QH^2 = (7,7)^2
QH^2 = (7,7)^2 - x^2
QH = √[(7,7)^2 - x^2]
Теперь давайте посмотрим на треугольник QKL. У него сторона KL равна QL, а сторона QK - нужно вычислить.
Мы можем использовать теорему Пифагора, чтобы найти значения сторон QKL: QK^2 + QH^2 = KL^2
Подставляем известные значения:
QK^2 + (QH)^2 = QL^2
QK^2 + (√[(7,7)^2 - x^2])^2 = (51,5)^2
QK^2 + (7,7)^2 - x^2 = (51,5)^2
QK^2 = (51,5)^2 - (7,7)^2 + x^2
QK = √[(51,5)^2 - (7,7)^2 + x^2]
Теперь давайте рассмотрим треугольник SKQ. У него сторона SQ равна x, а сторона SK - нужно вычислить.
В параллелограмме противоположные стороны равны, поэтому SK = QL.
Таким образом, SK = QL = 51,5 см.
Теперь у нас есть две выражения для SK в треугольниках SQH и SKQ, QK в треугольнике QKL, и SH, которое мы знаем.
Мы можем записать уравнение, используя эти значения:
SK + KH = SQ
51,5 + 12,5 = SQ
64 = SQ
Таким образом, SQ равна 64 см.
Теперь давайте сверим наше решение. Мы использовали свойства параллелограммов и теорему Пифагора для вычисления сторон и нашли, что SQ равно 64 см.
Надеюсь, мое объяснение было достаточно подробным и понятным. Если у вас есть еще вопросы или нужна дополнительная помощь, пожалуйста, сообщите мне.