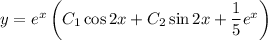В прямой треугольной призме АВСА1В1С1 в основании – прямоугольный треугольник, катеты которого равны 12дм и 5дм, а высота призмы равна 16дм. Найдите: объем призмы, площади боковой и полной поверхности призмы.
Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами, общим решением которого является .
1) — общее решение соответствующего линейного однородного дифференциального уравнения:
Применим метод Эйлера: сделаем замену где — некоторая постоянная. Тогда
Получили характеристическое уравнение:
Разделим обе части уравнения на :
Отрицательный дискриминант означает, что корни данного уравнения будут комплексно-сопряженными:
Тогда
Воспользуемся формулой Эйлера:
Фундаментальная система решений: — функции линейно независимые, поскольку
Общее решение:
2) — частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции .
Здесь , причем , поэтому частное решение имеет вид , где — неизвестный коэффициент, который нужно найти.
Тогда и подставим в исходное ЛНДР и найдем :
Разделим обе части уравнения на
Таким образом, частное решение:
Тогда общим решением исходного ЛНДР с постоянными коэффициентами:
Вычислить площадь фигуры ограниченной линиями
1) y =2,y=3x-x^2
Ищем пределы интегрирования:
3x-x² = 2
х² -3х +2 = 0
х = 1 и 2 ( по т. Виета)
S =₁∫²(3x-x^2 -2) dx = (3x²/2 -x³/3 -2x)|₁² = 6 - 8/3 - 4 - 3/2 +1/3 +2 =
=2,5 -7/3 = 2,5 - 2 1/3 = 1/6
2)y=-x^2+6x, y=0
Ищем пределы интегрирования:
-х² +6х = 0
х =0 и х = 6
S = ₀∫⁶ (-x² + 6x)dx = (-x³/3 +3х²)|₀⁶ = 36
3)y=-2sin x, y=sin x, 0 ≤ х ≤ п/3
Ищем пределы интегрирования:
-2Sinx= Sinx
-3Sinx = 0
Sinx = 0
₀∫π/3 Sinxdx = -Cosx|₀π/3 = -Cosπ/3 + Сos0 = -1/2 + 1 = 1/2
Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами, общим решением которого является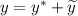 .
.
1)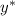 — общее решение соответствующего линейного однородного дифференциального уравнения:
— общее решение соответствующего линейного однородного дифференциального уравнения:
Применим метод Эйлера: сделаем замену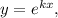 где
где 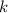 — некоторая постоянная. Тогда
— некоторая постоянная. Тогда 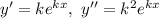
Получили характеристическое уравнение:
Разделим обе части уравнения на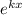 :
:
Отрицательный дискриминант означает, что корни данного уравнения будут комплексно-сопряженными:
Тогда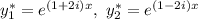
Воспользуемся формулой Эйлера: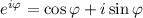
Фундаментальная система решений: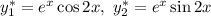 — функции линейно независимые, поскольку
— функции линейно независимые, поскольку 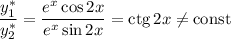
Общее решение: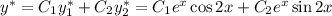
2)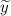 — частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции
— частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции 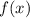 .
.
Здесь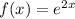 , причем
, причем 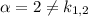 , поэтому частное решение имеет вид
, поэтому частное решение имеет вид 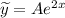 , где
, где 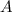 — неизвестный коэффициент, который нужно найти.
— неизвестный коэффициент, который нужно найти.
Тогда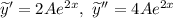 и
и 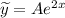 подставим в исходное ЛНДР и найдем
подставим в исходное ЛНДР и найдем 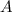 :
:
Разделим обе части уравнения на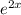
Таким образом, частное решение: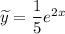
Тогда общим решением исходного ЛНДР с постоянными коэффициентами:
ответ: