В треугольник с основанием AC= 17 см и высотой BD= 5 см вписан квадрат KLMN так, что сторона KN лежит на основании AC, а вершины L и M — соответственно на сторонах AB и BC. Определи длину стороны квадрата. Длина стороны квадрата равна ... см.
В данном уравнении выражение 2х представляет собой неизвестное делимое.
2х = 5/6 * 36 = (5 * 36) / 6 = 180/6 = 30;
Для нахождения его значения мы частное, равное 5/6 умножаем на значение делителя 36. При умножении обыкновенной дроби на целое число мы должны это число умножитель на числитель. Затем полученный результат разделить на знаменатель.
2х = 30;
Последним действием мы делим произведение, равное 30 на значение второго множителя 2.
Пошаговое объяснение:
№18
s=πr² D=2r, где s - площадь окружности, r- радиус окружности, D - диаметр окружности
D=20дм
π=3,14
r=20/2=10дм
s=3,14*10²=314дм²
ответ: 314дм²
№19
s=πr², где s - площадь окружности, r- радиус окружности
s=706,5см²
π=3,14
r=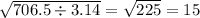 см
см
ответ: 15см
№20
s=πr² D=2r, где s - площадь окружности, r- радиус окружности, D - диаметр окружности
s=314см²
π=3,14
r=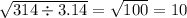 см
см
D=10*2=20см
ответ: 20см
№21
s=πr²
π(4r)²=π16r=16s
ответ: 16 раз
№22
D=2r
36s=π36r²=π(6r)² то есть радиус надо увеличить в 6 раз, а значит и диаметр нужно увеличить в 6 раз
ответ: в 6 раз
(не мое)
Пошаговое объяснение:
2х / 36 = 5/6;
В данном уравнении выражение 2х представляет собой неизвестное делимое.
2х = 5/6 * 36 = (5 * 36) / 6 = 180/6 = 30;
Для нахождения его значения мы частное, равное 5/6 умножаем на значение делителя 36. При умножении обыкновенной дроби на целое число мы должны это число умножитель на числитель. Затем полученный результат разделить на знаменатель.
2х = 30;
Последним действием мы делим произведение, равное 30 на значение второго множителя 2.
х = 30 / 2;
х = 15;
ответ: 15.