Вариант 8 xt 2017
1. в равнобедренной трапеции oacb ми n– середина сторон bc = 2, ac = 2.
острый угол трапеции 60°. определить угол между векторами ом и on.
2. через фокус параболы у* = -4х проведена прямая под углом 120° к оси ох.
написать уравнение прямой и найти длину образовавшейся хорды.
3. найти точку пересечения медиан и точку пересечения высот треугольника, вершины
которого а(-4; 2), b(2; -5), c(5; 0).
4. эллипс, симметричный относительно осей координат, фокусы которого находятся
на оси ох, проходит через точку м(-4; 21) и имеет эксцентриситет є = 3/4.
написать уравнение эллипса и найти фокальные радиус-вектора точки м.
5. написать уравнения перпендикуляра, опущенного из точки (2; 1; 0) на прямую
х = 3z -1
| y = 27
6. написать уравнение плоскости, проходящей через точки (0; –5; 0) и (0; 0; 2) и
перпендикулярной, к плоскости x+5 y + 27 -10 = (0).

хоть что нибудь !

Показать ответ

Ответ:

Роорш

19.01.2020 15:30

Построим правильную треугольную призму АВСА1В1С1 и проведем диагональ боковой грани А1В.

Правильная треугольная призма — призма, в основаниях которой лежат два правильных треугольника, а все боковые грани строго перпендикулярны этим основаниям.

Формула площади боковой поверхности призмы S=p*h, где р - периметр основания, h – высота

р=3*3=9 см (так как призма правильная)

Найдем высоту данной призмы АА1:

Рассмотрим треугольник АВА1:

Угол ВАА1 – прямой (так как призма правильная),

АВ=3 см – катет данного треугольника

ВА1=5 см – гипотенуза данного треугольника

По теореме Пифагора найдем второй катет:

АА1=√(ВА1^2 – AB^2)=√(5^2-3^2)=√(25-9)=√16=4 см

Боковая площадь данной призмы равна

S=p*h=9*4=36 кв. см.

Вычислите площадь боковой поверхности правильной треугольной призмы, если сторона основания равна 3

0,0(0 оценок)

Ответ:

snoopelol5

30.06.2020 08:05

№1.

Как проверить: подставляем координаты в уравнение. Если все совпадает - пара является решением уравнения, если нет - то нет.

(3;1)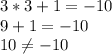 $3*3+1=-10\\9+1=-10\\10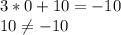\neq -10$

(0;10) $3*0+10=-10\\10\neq -10$

(2;4)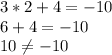 $3*2+4=-10\\6+4=-10\\10\neq -10$

(3;2,5)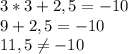 $3*3+2,5=-10\\9+2,5=-10\\11,5\neq -10$

ответ: если дано уравнение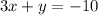 3x+y=-10 , то ни одна пара не является решением уравнения; если дано уравнение 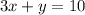3x+y=10 , то подходят пары (3;1), (0;10) (2;4).