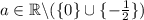Заметим, что, если x₀(a) - решение данного уравнения, то -x₀(a) также является решением уравнения. Поэтому при всех a таких, что x≠0, уравнение имеет не менее двух решений. Отсюда легко вывести, что a≠0;
Сделаем замену: m=x²; Так как m+m²≥0, то исходное уравнение (относительно m) равносильно следующему:
; Мы видим, что уравнение имеет единственное решение относительно m для данного a (при всех a, при которых выражение имеет смысл); Значит уравнение относительно x имеет ровно два решения. Осталось рассмотреть случай:
Множество А состоит из трех элементов:
А = {Атлантический; Индийский; Тихий}
Общее свойство: все элементы - океаны.
Его можно назвать "Океаны".
Множество В состоит из четырех элементов:
В = {Жайык; Иле; Ертис; Шу}
Общее свойство: все элементы - реки.
Его можно назвать "Реки".
Множество С состоит из пяти элементов:
С = {Моря; Озёра; Реки; Ледники; Океаны}
Общее свойство: все элементы входят в водную оболочку Земли.
Его можно назвать "Гидросфера".
Множество А является подмножеством множества С:
А ⊂ С
Множество В является подмножеством множества С:
В ⊂ С.
Заметим, что, если x₀(a) - решение данного уравнения, то -x₀(a) также является решением уравнения. Поэтому при всех a таких, что x≠0, уравнение имеет не менее двух решений. Отсюда легко вывести, что a≠0;
Сделаем замену: m=x²; Так как m+m²≥0, то исходное уравнение (относительно m) равносильно следующему:
1+2a≠0 ⇔ a≠-0.5;
ОТВЕТ: