Пусть треугольник АВС, биссектриса ВЕ и медиана АД. О- точка пересечения ВЕ и АД. Стороны напротив углов а,в,с, соответственно.
АВД -равнобедренный, ткт ВО -и биссектриса и высота. ВД=ДВ
Значит ВС=2АВ а=2с.
АО=ОД=8 (высота делит пополпам АД).Проведем ДМ до пересечения с АС. ДМ -средняя линия в ВЕС равна половине ВЕ и равна 8. ОЕ - средняя линия в АДМ и равна 4. АЕ*АЕ=8*8+4*4=16*5 АЕ=4*sqrt(5) EC=2*AE==8*sqrt(5) (по свойству биссектрисы)
Пусть O - точка пересечения AD и BE, тогда BO - высота и биссектриса ΔABD ⇒ ΔABD - равнобедренный (AB = BD) и BO - медиана ⇒ AO = OD = 8, BC = 2AB
Заметим, что в ΔABC: EC ÷ AE = BC ÷ AB = 2 ( свойство биссектрисы BE) ⇒ EC = 2AE ⇒ AC = AE + EC = 3AE
Проведем через точку C прямую, параллельную AB, а через точку B прямую, параллельную AC, то есть достроим ΔABC до параллелограмма ABMC, где M - точка пересечения проведенных прямых, тогда точка D - пересечение диагоналей построенного параллелограмма.
Рассмотрим ΔAOE и ΔBOM, они подобны по 2-м углам ⇒ BO ÷ OE = BM ÷ AE. Учитывая, что BM = AC получаем BO ÷ OE = 3.
Пусть OE = x, тогда BO = 3x; x + 3x = 16; 4x = 16; x = 4 ⇒ OE = 4; BO = 12
по теореме Пифагора из ΔABO: AB² = 8² + 12² = 208 ⇒ AB = 4√13; BC = 8√13
по теореме Пифагора из ΔAOE: AE² = 8² + 4² = 80 ⇒ AE = 4√5 ⇒ AC = 12√5
Пусть O точка пересечений биссектрисы BE и медианы AD. По условию BE⊥AD, откуда следует что BO биссектриса и высота, следовательно, треугольник ABD равнобедренный: AB=BD и BO медиана. Отсюда
AO=OD=AD/2=16/2=8.
Проведём DF так, чтобы DF║BE. Так как AD медиана, то BD=DC, следовательно DF средняя линия в треугольнике BEC. Отсюда, по свойству средней линии
DF=BE/2=16/2=8.
По построению OE║FD. Так как BO медиана, то AO=OD, следовательно OE средняя линия в треугольнике ADF. Отсюда, по свойству средней линии
OE=DF/2=8/2=4.
По условию BE⊥AD, что и OE⊥AD. Тогда треугольник AOE прямоугольный с гипотенузой AE. Применим теорему Пифагора:
AE²=AO²+OE²=8²+4²=64+16=80=4²·5,
откуда
По условию BE - биссектриса и по свойству биссектрисы
Как отметили ранее, AB=BD=BC/2 и BD=DC, то есть BC=2·AB. Поэтому
Теперь можем найти
(ед.).
Используя OE=4 находим
BO=BE-OE=16-4=12.
Так как BE⊥AD, то треугольник AOB прямоугольный с гипотенузой AB. Применим теорему Пифагора:
АВ=4*sqrt(13)
ВС=8*sqrt(13)
АС= 12*sqrt(5)
Пошаговое объяснение:
Пусть треугольник АВС, биссектриса ВЕ и медиана АД. О- точка пересечения ВЕ и АД. Стороны напротив углов а,в,с, соответственно.
АВД -равнобедренный, ткт ВО -и биссектриса и высота. ВД=ДВ
Значит ВС=2АВ а=2с.
АО=ОД=8 (высота делит пополпам АД).Проведем ДМ до пересечения с АС. ДМ -средняя линия в ВЕС равна половине ВЕ и равна 8. ОЕ - средняя линия в АДМ и равна 4. АЕ*АЕ=8*8+4*4=16*5 АЕ=4*sqrt(5) EC=2*AE==8*sqrt(5) (по свойству биссектрисы)
АС=12*sqrt(5)
ВО=16-4=12. АВ*АВ=8*8+12*12=16*13 АВ=4*sqrt(13)
ВС=2*АВ=8*sqrt(13)
Дано:
ΔABC
BE - биссектриса, AD - медиана
BE ⊥ AD
BE = AD = 16
Найти:
стороны ΔABC
Пусть O - точка пересечения AD и BE, тогда BO - высота и биссектриса ΔABD ⇒ ΔABD - равнобедренный (AB = BD) и BO - медиана ⇒ AO = OD = 8, BC = 2AB
Заметим, что в ΔABC: EC ÷ AE = BC ÷ AB = 2 ( свойство биссектрисы BE) ⇒ EC = 2AE ⇒ AC = AE + EC = 3AE
Проведем через точку C прямую, параллельную AB, а через точку B прямую, параллельную AC, то есть достроим ΔABC до параллелограмма ABMC, где M - точка пересечения проведенных прямых, тогда точка D - пересечение диагоналей построенного параллелограмма.
Рассмотрим ΔAOE и ΔBOM, они подобны по 2-м углам ⇒ BO ÷ OE = BM ÷ AE. Учитывая, что BM = AC получаем BO ÷ OE = 3.
Пусть OE = x, тогда BO = 3x; x + 3x = 16; 4x = 16; x = 4 ⇒ OE = 4; BO = 12
по теореме Пифагора из ΔABO: AB² = 8² + 12² = 208 ⇒ AB = 4√13; BC = 8√13
по теореме Пифагора из ΔAOE: AE² = 8² + 4² = 80 ⇒ AE = 4√5 ⇒ AC = 12√5
Пошаговое объяснение:
Дано (см. рисунок):
ΔABC
BE - биссектриса
AD - медиана
BE⊥AD
BE=AD=16 (ед.)
Найти AB, BC, CA.
Решение.
Пусть O точка пересечений биссектрисы BE и медианы AD. По условию BE⊥AD, откуда следует что BO биссектриса и высота, следовательно, треугольник ABD равнобедренный: AB=BD и BO медиана. Отсюда
AO=OD=AD/2=16/2=8.
Проведём DF так, чтобы DF║BE. Так как AD медиана, то BD=DC, следовательно DF средняя линия в треугольнике BEC. Отсюда, по свойству средней линии
DF=BE/2=16/2=8.
По построению OE║FD. Так как BO медиана, то AO=OD, следовательно OE средняя линия в треугольнике ADF. Отсюда, по свойству средней линии
OE=DF/2=8/2=4.
По условию BE⊥AD, что и OE⊥AD. Тогда треугольник AOE прямоугольный с гипотенузой AE. Применим теорему Пифагора:
AE²=AO²+OE²=8²+4²=64+16=80=4²·5,
откуда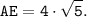
По условию BE - биссектриса и по свойству биссектрисы
Как отметили ранее, AB=BD=BC/2 и BD=DC, то есть BC=2·AB. Поэтому
Теперь можем найти
Используя OE=4 находим
BO=BE-OE=16-4=12.
Так как BE⊥AD, то треугольник AOB прямоугольный с гипотенузой AB. Применим теорему Пифагора:
AB²=AO²+OB²=8²+12²=64+144=208=4²·13,
откуда
Из AB=BC/2 находим: