При ;
Таким образом, можно переписать предел:
; Удобно сделать замену: ; Предел получится таким:
; Воспользуемся следующим фактом: При этом ; Тогда: ; Последний предел очевиден:
При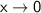
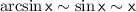 ;
;
Таким образом, можно переписать предел: