S=
Пошаговое объяснение:
Для определения пределов интегрирования находим координаты пересечения графиков по оси х
-х²+9=5
-х²=-4
х1=2
х2=-2
График в файле.
S=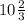
Пошаговое объяснение:
Для определения пределов интегрирования находим координаты пересечения графиков по оси х
-х²+9=5
-х²=-4
х1=2
х2=-2
График в файле.