Смотри, тут самое главное - знать таблицу производных.
От 1' = 0
От e^(-x) будет -e^x, но т.к. у тебя еще перед формулой стоит минус, то производная будет просто e^x
От х' = 1
От сos(x)' = -sin(x)
От sin(x)' = cos(x)
Когда нашел первую производную числителя и знаменателя, то подставил снова 0, все равно выходит неопределенность вида , значит снова находим производную... И так делаем до тех пор, пока не найдем результат.
ответ: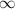
Пошаговое объяснение:
Смотри, тут самое главное - знать таблицу производных.
От 1' = 0
От e^(-x) будет -e^x, но т.к. у тебя еще перед формулой стоит минус, то производная будет просто e^x
От х' = 1
От сos(x)' = -sin(x)
От sin(x)' = cos(x)
Когда нашел первую производную числителя и знаменателя, то подставил снова 0, все равно выходит неопределенность вида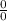 , значит снова находим производную... И так делаем до тех пор, пока не найдем результат.
, значит снова находим производную... И так делаем до тех пор, пока не найдем результат.