и -2
Пошаговое объяснение:
Подставим в уравнение известный корень (-2). Получаем:
Преобразуем выражение:
И, таким образом, найдём k.
Теперь подставим известное k в изначальное уравнение.
Перед нами квадратное уравнение (вида )
Вычислим дискриминант по формуле :
Дискриминант положительный, а значит, будет два корня.
Теперь найдём оба корня по формулам:
Итак, корни уравнения .
x₁ = -2
x₂ = -1,5
x² - 7kx + 3 = 0
(-2)² - 7k(-2) + 3 = 0
4 + 14k + 3 = 0
14k = -7
k = -7/14
k = -1/2 → подставим значение k в уравнение:
x² - 7*(-1/2)x + 3 = 0
x² + 3,5x + 3 = 0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = (3,5)² - 4·1·3 = 12,25 - 12 = 0,25
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x₁ = ( -3.5 - √0.25)/ 2·1 = (-3.5 - 0.5)/2 = -4/2 = -2
x₂ = (-3.5 + √0.25)/2·1 = (-3.5 + 0.5)/2 = -3 2 = -1,5
Пошаговое объяснение:
Подставим в уравнение известный корень (-2). Получаем:
Преобразуем выражение:
И, таким образом, найдём k.
Теперь подставим известное k в изначальное уравнение.
Перед нами квадратное уравнение (вида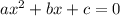 )
)
Вычислим дискриминант по формуле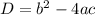 :
:
Дискриминант положительный, а значит, будет два корня.
Теперь найдём оба корня по формулам:
Итак, корни уравнения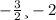 .
.
x₁ = -2
x₂ = -1,5
Пошаговое объяснение:
x² - 7kx + 3 = 0
(-2)² - 7k(-2) + 3 = 0
4 + 14k + 3 = 0
14k = -7
k = -7/14
k = -1/2 → подставим значение k в уравнение:
x² - 7*(-1/2)x + 3 = 0
x² + 3,5x + 3 = 0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = (3,5)² - 4·1·3 = 12,25 - 12 = 0,25
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x₁ = ( -3.5 - √0.25)/ 2·1 = (-3.5 - 0.5)/2 = -4/2 = -2
x₂ = (-3.5 + √0.25)/2·1 = (-3.5 + 0.5)/2 = -3 2 = -1,5