Задание 3
Найдите чертежи и уравнения, соответствующие каждому отчету.
а) между городом и центром подготовки космонавтов – 330 км. Курсант для выезда из города в центр сначала сидел в автобусе со скоростью 75 км/ч. Остальные 30 км дороги проехали на машине, где встречается дорога. Сколько часов Курсант ездил на автобусе?

Б) между городом и центром подготовки космонавтов – 330 км. Курсант ходил 4 часа на автобусе со скоростью 75 км/ч для выезда из города в центр. Остальные дороги проехали на машине, где встречается дорога. Сколько путей Студент шел на машине?

Это соответствует чертежу и приведению ниже.

75∙ х + 30 = 330х + 75 ∙ 3 = 33075 ∙ х - 30 = 33075 ∙ 30 + х = 330
Это соответствует чертежу и приведению ниже.

75 ∙ х + 4 = 33075 ∙ 4 + х = 33075 ∙ х - 4 = 33075 ∙ 4 + х = 3307

Я немного не поняла запись уравнения, поэтому не судите строго, потому что я начну решать так уравнение, как я его поняла. Для начала раскроем скобки там, где они есть. Запишем вот так: 6*2x+6*(-1)+2*4x+2*(-3)=17. Теперь всё умножение вычислим. Получается так: 12x+(-6)+8x+(-6)=17. Теперь доконца раскроем скобки: 12x-6+8x-6=17. Приведём подобные слагаемые: 12x+8x-6-6=17. Теперь вычислим всё, что возможно: 20x-12=17. Так как число «-12» и число «17» являются подобными, можно их вычислить, но нужно перенести число «-12» в правую часть и сменить знак: 20x=17+12. Всё вычислим: 20x=29. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель: x = 29:20. Всё вычислим и запишем в ответ результат. ответ: x=29/20=1 9/20 или 1,45.

Пусть сторона квадрата равна a; В начальный момент времени все находятся в одной вершине квадрата.

Заметим, что скорость второй машины ровно в три раза превосходит скорость первой. Тогда первый обгон между двумя машинами случится тогда, когда первая проедет 2a (вторая проедет 3×2a=6a); Поэтому все обгоны между машинами будут в вершинах.

Пусть скорость велосипеда равна v;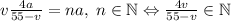 (i); Аналогично

(ii); (*); Также (**); Переставляя элементы в (i) получим равносильное утверждение: ;

Рассмотрим  числа n и n+4: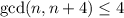 ; Рассмотрим все нечетные n; Тогда n и n+4 взаимно просты, а значит 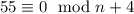; Получаем числа n∈{1,7,51}; Рассмотрим числа n такие, что

; Тогда ; Получаем числа n∈{6,18,106}; Осталось рассмотреть числа n, такие, что

; Отсюда  ;

Тогда n∈{16,40,216}; Всего: n∈{1,6,7,16,18,40,51,106,216};

;

Условию (ii) удовлетворяет только число 33;

ответ: 33 км/ч