Обозначим частное за . Тогда из условия можно сделать вывод, что делитель равен , а делимое равно .
Так как {делимое} / {делитель} = {частное}, то:
И решаем данное уравнение (помня, что ):
Квадратное уравнение можно решить множеством
Например, можно применить теорему Виета (она гласит, что в данном случае и ). Так как делится нацело на не такое уж большое количество чисел, то можно сделать вывод, что и .
Можно и решить дискриминантом (хотя это в данном случае несколько сложнее в плане вычислений):
Обозначим частное за
. Тогда из условия можно сделать вывод, что делитель равен 
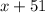, а делимое равно 
.
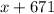Так как {делимое} / {делитель} = {частное}, то:
И решаем данное уравнение (помня, что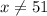
):
Квадратное уравнение можно решить множеством
Например, можно применить теорему Виета (она гласит, что в данном случае
и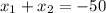 
). Так как 
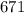делится нацело на не такое уж большое количество чисел, то можно сделать вывод, что 
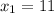и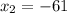 
.
Можно и решить дискриминантом (хотя это в данном случае несколько сложнее в плане вычислений):
Таким образом, это могло быть одно из чисел
и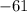 
:
Задача решена!
ответ: 11 или - 61 .a : b = 2 : 3 - отношение первого числа ко второму
b : c = 2/3 : 8/5 = 10 : 24 - отношение второго числа к третьему
(Общий знаменатель 15: 2/3 = 10/15; 8/5 = 24/15)
3 : 10 = 0,3 - доп. множ. ко второй пропорции (чтобы уравнять b)
b : c = (10·0,3) : (24·0,3) = 3 : 7,2 - отношение второго числа к третьему
а : b : c = 2 : 3 : 7,2 - отношение трёх чисел
Пусть х - коэффициент пропорциональности, тогда а = 2х, b = 3х, с = 7,2х. Сумма наибольшего и наименьшего числа равна 46. Уравнение:
7,2х + 2х = 46
9,2х = 46
х = 46 : 9,2
х = 5
а = 2х = 2 · 5 = 10 - наименьшее число
b = 3х = 3 · 5 = 15 - второе число
с = 7,2х = 7,2 · 5 = 36 - наибольшее число
ответ: числа 10, 15 и 36.