Женя и Сеня играют в игру «крестики-крестики». Игра заключается в том, что Женя и Сеня по очереди ставят крестики на доску 55×55, при этом нельзя ставить 11 крестиков подряд по вертикали или по горизонтали (по диагонали можно). Какое наибольшее количество крестиков Женя и Сеня могут поставить на доску
1001.00
Пошаговое объяснение:
Все жители острова не могут быть лжецами, иначе каждый из них сказал бы правду. Возьмем некоторого рыцаря. Из его заявления вытекает, что лжецов на острове больше, чем (2001-1)/2=1000. Возьмем теперь некоторого лжеца. Его заяление ложно, поэтому кроме него не более половины жителей острова - лжецы. Это означает, что кроме него на острове не более 2000/2=1000 лжецов, т.е. вместе с ним лжецов не более 1001. Таким образом, из полученных оценок на число лжецов получаем, что единственная возможность - когда на острове ровно 1001 лжец.
Пошаговое объяснение:
Так как искомая дробь отличается от √5 максимум на 0,01, то она лежит в промежутке
Оценим √5: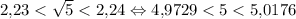
— верно. Тогда
Последовательно переберём натуральные n. m — натуральное число, поэтому между числами 2,22n и 2,25n должно находиться хотя бы одно натуральное число.
n = 1 — 2,22 < m < 2,25 — не подходит;
n = 2 — 4,44 < m < 4,5 — не подходит;
n = 3 — 6,66 < m < 6,75 — не подходит;
n = 4 — 8,88 < m < 9 — не подходит;
n = 5 — 11,1 < m < 11,25 — не подходит;
n = 6 — 13,32 < m < 13,5 — не подходит;
n = 7 — 15,54 < m < 15,75 — не подходит;
n = 8 — 17,76 < m < 18 — не подходит;
n = 9 — 19,98 < m < 20,25 — существует m = 20.
Проверим дробь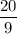
:
Неравенство не выполняется, значит, дробь не подходит.
n = 10 — 22,2 < m < 22,5 — не подходит;
n = 11 — 24,42 < m < 24,75 — не подходит;
n = 12 — 26,64 < m < 27 — не подходит;
n = 13 — 28,86 < m < 29,25 — существует m = 29.
Проверим дробь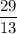
:
Значит, данная дробь нам подходит.