Знайко розставив у клітинки квадратної таблиці 3 х 3 попарно різні цифри таким чином, ще тризначні числа, які можна прочитати у рядках ціеї таблиці зліва направо та у стовлчикая верху вниз, діляться на 6. Скільки з цих шести чисел діляться на 5? Знайка расставил в клетки квадратной таблицы 3 х 3 попарно разные цифры таким образом, еще трехзначные числа, которые можно прочитать в строках этой таблицы слева направо и в стовлчикая верха вниз, делятся на 6. Сколько из этих шести чисел делятся на 5?

Пошаговое объяснение:

Расстояние между станциями 41 км.

Направление движения: противоположное.

Выехали из двух станций одновременно.

Скорость первого поезда на 13 км больше второго поезда.

Время движения 4 ч.

Расстояние между поездами 525 км.

Определить скорость второго поезда.

Перед решением, давай очень внимательно разберемся с условием задачи.

Из двух станций, расстояние между которыми 41 км, одновременно в противоположных направлениях выехали 2 поезда. Скорость первого поезда на 13 км/ч больше скорости второго поезда. Время движения поездов 4 ч, и расстояние между ними после выезда стало 525 км. Поезда двигались в разных направлениях, значит за 4 часа каждый поезд, двигаясь со своей скоростью, проехал свое расстояние. Согласно условию задачи, в начале движения между поездами расстояние уже было 41 км, значит фактически оба поезда проехали 525 – 41 = 484 км.

Примем скорость второго поезда (v1) за х км/ч. Тогда скорость первого поезда (v2) равна (х +13) км/ч.

Расстояние, на которое удаляются поезда за единицу времени, называют скоростью удаления vуд.

В этом случае скорость удаления vуд = v1 + v2, км/ч

Через t часов между поездами будет расстояние:

Sуд = vуд * t = (v1 + v2) * t, км

Составим уравнение:

(х + (х + 13)) * 4 = 484

(х + х + 13) * 4 = 484

(2х + 13) * 4 = 484

8х + 52 = 484

8х = 484 – 52

8х = 432

х = 432 : 8

х = 54

Скорость второго поезда равно 54 км/ч.

Скорость первого поезда равно: 54 + 13 = 67 км/ч.

ответ: скорость второго поезда 54 км/ч.

Проверка:

Определим расстояние, которое проехал каждый поезд по формуле:

S = v * t, где s — пройденный путь (км), v — скорость движения (км/ч), t — время (ч), за которое пройден путь S.

Расстояние, которое проехал первый поезд:

S1 = 67 * 4 = 268 км.

Расстояние, которое проехал второй поезд:

S2 = 54 * 4 = 216 км.

Сумма расстояний, которые проехал первый поезд и расстояние, которое проехал второй поезд, фактически проехали два поезда.

S3 = S1 - S2, км

S3 = 268 + 216 = 484 км.

В начале движения между поездами расстояние уже было 41 км, значит расстояние между поездами составит: 484 + 41 = 525 км.

Задача решена верно.

Скорость второго поезда 54 км/час

Пошаговое объяснение:

Общее расстояние станций - 41 км

Поезд с А проезжает на 13км больше чем поезд Б

С какой скоростью ехал второй поезд, через 4 часа после выезда расстояние между ними стало равно 525 км.

U2 - ?

U1 = 13 км/час > S2

t = 4 часа

S = 525 км, но так как расстояние было ещё 41 км, то мы должны от 525 отнять 41 и получим 484 км. Тоесть 484 км они проехали без расстояние от станции.

Решение

Теперь найдём общую скорость с формулы:

S = U*t  >>  U =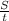 = = 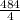121 км/час - общая скорость, но т.к. сказано что первый поезд двигался на 13 км/час быстрее чем второй. Значит:

U1 =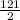 + 6,5 = 67 - скорость первого поезда, а скорость второго будет:

U2 =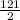 - 6,5 = 54 - скорость второго поезда.

Теперь проверим: (67+54) * 4 = 484 км - теперь прибавим 41 км и получим 525 км, то есть условие выполнено, скорость второго поезда на 13 км меньше чем скорость первого, получилось выполнить условие задачи.