– согласно правилу Лопиталя.
Находим производные: (tg4x)' = ;
(sin6x)' = 6*cos6x ⇒ исходный предел равен:
ответ: данный предел равен
2/3
Пошаговое объяснение:
Находим производные: (tg4x)' =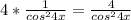 ;
;
(sin6x)' = 6*cos6x ⇒ исходный предел равен:
ответ: данный предел равен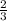
2/3
Пошаговое объяснение: