подбираем 1 корень:
x=1
тогда этот многочлен можно представить как:
(x-1)(3x^2+ax+b)=3x^3+ax^2+bx-3x^2-ax-b=3x^3+x^2(a-3)+x(b-a)-b
известно, что:
3x^3+x^2-3x-1=3x^3+x^2(a-3)+x(b-a)-b
тогда составляем систему:
a-3=1
b-a=-3
b=1
решаем:
a=1+3=4
тогда:
3x^3+x^2-3x-1=(x-1)(3x^2+4x+1)
раскладываем на множители 3x^2+4x+1
3x^2+4x+1=0
D=16-12=4
x1=(-4+2)/6=-1/3
x2=-1
3x^2+4x+1=3(x+1)(x+1/3)=(x+1)(3x+1)
в итоге исходный многочлен разложится на множители:
3x^3+x^2-3x-1=(x-1)(x+1)(3x+1)
(。_。)
простите если не так я просто не специалист
а)
б) 324
Объяснение:
И числитель и знаменатель это формула сокращенного умножения, а точнее разница квадратов. Раскладывается следующим образом:
a² - b² = (a - b) × (a + b)
Сначала разберемся с числителем:
1) 17.5² - 9.5² = (17.5 - 9.5) × (17.5 - 9.5)
2) (17.5 - 9.5) × (17.5 - 9.5) = (8) × (27); (в конце скобки писать не обязательно, это я для наглядности)
Так и оставим пока что. Далее действия со знаменателем:
1) 131.5² - 3.5² = (131.5 - 3.5) × (131.5 + 3.5)
2) (131.5 - 3.5) × (131.5 + 3.5) = (128) × (135); (в конце скобки писать не обязательно, это я для наглядности)
Подставляем числитель и знаменатель:
8 и 128 сокращаются. Так же 27 и 135 сокращаются:
б)
В числителе находится формула сокращенного умножения, а точнее сумма кубов. Раскладывается следующим образом:
а³ + b³ = (a + b) × (a² - ab + b³)
Разберемся с числителем:
1) 59³ + 43³ = (59 + 41) × (59² - 59 × 41 + 41²)
2) (59 + 41) × (59² - 59 × 41 + 41²) = (100) × (59² - 59 × 41 + 41²)
Так пока и оставим (100 не обязательно брать в скобки, это я для наглядности).
Поставим получившийся пример обратно в числитель:
100 и 100 сокращаются:
59² - 59 × 41 + 41² - 59 × 41 = 59² + 41² - 59 × 41 - 59 × 41 (от перемены мест слагаемых сумма не изменяется)
59² + 41² - 59 × 41 - 59 × 41 = 59² - 2 (59 × 41) + 41²
Это разложенный вид формули сокращенного умножения, а точнее квадрата разницы. Складывается следующим образом:
a² - 2ab + b² = (a - b)²
59² - 2 (59 × 41) + 41² = (59 - 41)² = 18² = 324
подбираем 1 корень:
x=1
тогда этот многочлен можно представить как:
(x-1)(3x^2+ax+b)=3x^3+ax^2+bx-3x^2-ax-b=3x^3+x^2(a-3)+x(b-a)-b
известно, что:
3x^3+x^2-3x-1=3x^3+x^2(a-3)+x(b-a)-b
тогда составляем систему:
a-3=1
b-a=-3
b=1
решаем:
b=1
a=1+3=4
тогда:
3x^3+x^2-3x-1=(x-1)(3x^2+4x+1)
раскладываем на множители 3x^2+4x+1
3x^2+4x+1=0
D=16-12=4
x1=(-4+2)/6=-1/3
x2=-1
3x^2+4x+1=3(x+1)(x+1/3)=(x+1)(3x+1)
в итоге исходный многочлен разложится на множители:
3x^3+x^2-3x-1=(x-1)(x+1)(3x+1)
(。_。)
простите если не так я просто не специалист
а)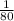
б) 324
Объяснение:
а)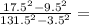
И числитель и знаменатель это формула сокращенного умножения, а точнее разница квадратов. Раскладывается следующим образом:
a² - b² = (a - b) × (a + b)
Сначала разберемся с числителем:
1) 17.5² - 9.5² = (17.5 - 9.5) × (17.5 - 9.5)
2) (17.5 - 9.5) × (17.5 - 9.5) = (8) × (27); (в конце скобки писать не обязательно, это я для наглядности)
Так и оставим пока что. Далее действия со знаменателем:
1) 131.5² - 3.5² = (131.5 - 3.5) × (131.5 + 3.5)
2) (131.5 - 3.5) × (131.5 + 3.5) = (128) × (135); (в конце скобки писать не обязательно, это я для наглядности)
Подставляем числитель и знаменатель:
8 и 128 сокращаются. Так же 27 и 135 сокращаются:
б)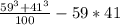
В числителе находится формула сокращенного умножения, а точнее сумма кубов. Раскладывается следующим образом:
а³ + b³ = (a + b) × (a² - ab + b³)
Разберемся с числителем:
1) 59³ + 43³ = (59 + 41) × (59² - 59 × 41 + 41²)
2) (59 + 41) × (59² - 59 × 41 + 41²) = (100) × (59² - 59 × 41 + 41²)
Так пока и оставим (100 не обязательно брать в скобки, это я для наглядности).
Поставим получившийся пример обратно в числитель:
100 и 100 сокращаются:
59² - 59 × 41 + 41² - 59 × 41 = 59² + 41² - 59 × 41 - 59 × 41 (от перемены мест слагаемых сумма не изменяется)
59² + 41² - 59 × 41 - 59 × 41 = 59² - 2 (59 × 41) + 41²
Это разложенный вид формули сокращенного умножения, а точнее квадрата разницы. Складывается следующим образом:
a² - 2ab + b² = (a - b)²
59² - 2 (59 × 41) + 41² = (59 - 41)² = 18² = 324