1. Теоретическая часть.

Отметь знаком «+» правильные утверждения и знаком «-» ошибочные.

1.Прямоугольным называется треугольник, у которого все углы прямые.

2. В прямоугольном треугольнике может быть только один прямой угол.

3. Сумма двух острых углов прямоугольного треугольника равна 100.

4. Катет прямоугольного треугольника, лежащий против угла в 30, равен половине гипотенузы.

5.Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого, то такие треугольники равны.

6. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

7. Перпендикуляр , проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой.

8. Все точки каждой из двух прямых равноудалены от другой прямой.

9. . Длина наклонной, проведенной из точки к прямой, называется расстоянием от этой точки до прямой.

2. Тестовая часть.

1. Если в ∆ АВС < А = 30 , < В = 90, АС= 20 см, то сторона ВС равна

а) 10 см ; б) 20 см ; в) 40 см.

2. . Если в ∆ АВС < А = 90, АВ = АС, то

а) < В = 55 ; б) < С = 45 ; в) < В = 65.

3.По чертежу найти < ВЕА , СЕ, АС, если ВЕ = 6 см. <А= 30°

В а) 120; 3см; 9см.

б) 110; 6см; 12см.

в) 100; 5см; 10см.

С Е А

3. Практическая часть.

1. В треугольнике АВС < С = 60, < В = 90. Высота ВВ1 = 2см. Найдите АВ.

2. В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF, причем FC = 13 см. Найдите расстояние от точки F до прямой DE.

Подобные одночлены - это одночлены, которые состоят из одних и тех же букв, в одинаковых степенях, но с разными или одинаковыми коэффициентами (числовыми множителями).

В этих выражениях требуется представить одинаковые множители как степень одного множителя.

1. -3,1*babab = -3,1*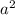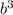, подобным ему будет 2/5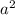

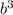
2. 2 1/3*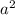ba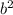*(-3) = -7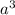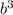, подобным ему будет -3,1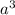

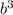
3. 1/5bab*2 = 2/5a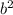, подобным ему будет -7a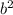

Похоже это задание на внимательность, чтобы правильно понимать смысл подобных одночленов и не вестись на одинаковые коэффициенты.

рассмотрим сначала многочлен

5 ⋅ x 2 ⋅ y + 2 ⋅ y 3 − x ⋅ y + 1 5·x2·y+2·y3−x·y+1

: его члены имеют стандартный вид, подобные члены отсутствуют, значит многочлен задан в стандартном виде, и никаких дополнительных действий не требуется.

Теперь разберем многочлен

0 , 8 + 2 ⋅ a 3 ⋅ 0 , 6 − b ⋅ a ⋅ b 4 ⋅ b 5 0,8+2·a3·0,6−b·a·b4·b5

. В его состав входят нестандартные одночлены: 2 ⋅ a 3 ⋅ 0 , 6 и − b ⋅ a ⋅ b 4 ⋅ b 5 2·a3·0,6 и −b·a·b4·b5, т.е. имеем необходимость привести многочлен к стандартному виду, для чего первым действием преобразуем одночлены в стандартный вид: 2 ⋅ a 3 ⋅ 0 , 6 = 1 , 2 ⋅ a 3 2·a3·0,6=1,2·a3; − b ⋅ a ⋅ b 4 ⋅ b 5 = − a ⋅ b 1 + 4 + 5 = − a ⋅ b 10 −b·a·b4·b5=−a·b1+4+5=−a·b10, таким образом получаем следующий многочлен: 0 , 8 + 2 ⋅ a 3 ⋅ 0 , 6 − b ⋅ a ⋅ b 4 ⋅ b 5 = 0 , 8 + 1 , 2 ⋅ a 3 − a ⋅ b 10 0,8+2·a3·0,6−b·a·b4·b5=0,8+1,2·a3−a·b10. В полученном многочлене все члены – стандартные, подобных членов не имеется, значит наши действия по приведению многочлена к стандартному виду завершены.