20.4. Задайте функцию у формулой с таблицы 20.6: Таблица 20.6
1)
1
2
3
2)
1
2
3
4
у
3
6
9
12
10
4
Y
13
3)
х
1
1
2
3
4
4)
1
1
4
2
3
2
у
5
8
-12
11
-3
у
-9
—6
5)
1
1
2
3
9
6)
4
1
х
4
2
-2
-8
-11
-4
-13
у
-7
у
-10​

ответ:Для того, чтобы найти при каком значении переменной x равны значения выражений (5x - 1)(2 - x) и (x - 3)(2 - 5x) составим и решим следующее уравнение.

(5x - 1)(2 - x) = (x - 3)(2 - 5x);

10x - 5x2 - 2 + x = 2x - 5x2 - 6 + 15x;

Перенесем в разные части уравнения слагаемые с переменными и без. При переносе слагаемых из одной части уравнения в другую меняем знаки слагаемых на противоположные.

-5x2 + 5x2 + 10x + x - 2x - 15x = -6 + 2;

x(10 + 1 - 2 - 15) = -4;

-6x = -4;

x = -4 : (-6);

x = 2/3.

ответ: x = 2/3

Подобное решение.

Объяснение:

Объяснение:

a) x² - 2x - 15 < 0

   x² + 3x - 5x - 15 > 0

   x(x + 3) - 5(x + 3) > 0

   (x + 3)(x - 5) > 0

   x + 3 < 0         x - 5 > 0

   x < -3              x > 5

   x ∈ (-∞, -3) ∪ (5, +∞)

б) -x² + 6x ≥ 0

   -x(x - 6) ≥ 0

   x(x - 6) ≤ 0

   x ≥ 0          x - 6 ≤ 0

                     x ≤ 6

   x ∈ [0, 6]

в)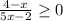

   4 - x ≤ 0         5x - 2 > 0

   x ≤ 4               5x > 2

                          x >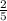

   x ∈ (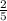, 4]

г) x(x - 9)(x + 2) > 0

   x < 0              (x - 9)(x + 2) > 0

                          x - 9 > 0             x + 2 > 0

                          x > 9                  x > -2

   x ∈ (-2, 0) ∪ (9, +∞)

д)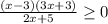  

    2x + 5 > 0                      (x - 3)(3x + 3) ≥ 0

    2x > -5                            x - 3 ≥ 0              3x + 3 ≤ 0

    x >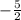                             x ≥ 3                    3x ≤ -3

                                                                       x ≤ -1

   x ∈ (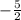 , -1] ∪[3, +∞)