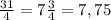Заметим, что числа 81 и 1/3 являются степенями числа 3.
Мы можем записать число 81 как 3^4, так как 3 в четвёртой степени равно 81.
То есть, уравнение приобретает вид: (3^4)^(x-8) = 3^(-1).
Для вычисления степени степени, мы должны умножить показатели степени.
Получаем следующее уравнение: 3^(4*(x-8)) = 3^(-1).
Теперь мы получили уравнение при совпадающей основе 3. Основное свойство степеней гласит, что если степени с одинаковыми основами равны, то и сами основы равны.
Из этого свойства следует, что 4*(x-8) = -1.
Теперь решим полученное уравнение:
4*(x-8) = -1
Раскроем скобку:
4x - 32 = -1
Добавим 32 к обеим сторонам уравнения:
4x = 31
Разделим обе стороны на 4:
x = 31/4.
Итак, решение уравнения 81^x-8 = 1/3 равно x = 31/4.
Надеюсь, я смог достаточно подробно и обстоятельно объяснить решение данного уравнения. Если у тебя возникнут дополнительные вопросы, не стесняйся задавать их!
Сначала преобразуем число 1/3 в степень числа 81.
Заметим, что числа 81 и 1/3 являются степенями числа 3.
Мы можем записать число 81 как 3^4, так как 3 в четвёртой степени равно 81.
То есть, уравнение приобретает вид: (3^4)^(x-8) = 3^(-1).
Для вычисления степени степени, мы должны умножить показатели степени.
Получаем следующее уравнение: 3^(4*(x-8)) = 3^(-1).
Теперь мы получили уравнение при совпадающей основе 3. Основное свойство степеней гласит, что если степени с одинаковыми основами равны, то и сами основы равны.
Из этого свойства следует, что 4*(x-8) = -1.
Теперь решим полученное уравнение:
4*(x-8) = -1
Раскроем скобку:
4x - 32 = -1
Добавим 32 к обеим сторонам уравнения:
4x = 31
Разделим обе стороны на 4:
x = 31/4.
Итак, решение уравнения 81^x-8 = 1/3 равно x = 31/4.
Надеюсь, я смог достаточно подробно и обстоятельно объяснить решение данного уравнения. Если у тебя возникнут дополнительные вопросы, не стесняйся задавать их!
0,482487
Объяснение:
(но это не точно)
x =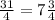 = 7,75
= 7,75
Объяснение:
81 = 3⁴
4x - 32 = -1, так как основания одинаковые
4х = -1 + 32
4х = 31
х =