Білім басқармасы. емтихандық жұмыс.9 сынып, жалпы білім – негізгі нұсқа, 2019 ж.нұсқа 11. ара қашықтығы 500 км. 2 қаладан, бір мезгілде қарама-қарсы трактор менжүк машинасы шықты. егер жүк машинасының ғы трактордыңғынан 4 есе артық болса, онда олар 4 сағаттан кейін кездеседі.трактордың ғын табыңдар.2. егер үшінші және жетінші мүшелерінің көбейтіндісі 114 тең болса, ондабесінші мүшесі нешеге тең болады? sin(a+b)+sin(a-3)3. тепе – теңдікті дәлелдеңіздер: sin(a+b)-sin(a-b) = tga.ctgß4. өрнекті ықшамданыздар: (х-2 x+2) 8x5- 5)5. берілген функциялар графиктерінің қилысу нүктелерін табыңдарy=x+3х және у = х2 + 36. теңсіздіктер жүйесін шешіңіздер: x* - 4х – 12.0x - 2 o!
Самый классический их решения, через дискриминант.
Во первых надо знать, что Квадратное уравнение имеет 2 корня (основная теорема алгебры).
Во вторых надо знать, что если число (дискриминант) под корнем отрицательно, то решения у уравнения нет.
В общем виде, квадратное уравнение выглядит так:
При этом
Поначалу находят дискриминант:
Если
Если
Если
После того как ты нашел сам дискриминант, используешь следующую формулу:
Если не понятно.
То вот:
Возможно, существует и другой метод доказательства, но я буду использовать метод от противного.
Итак, нужно доказать, что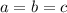
, то есть
Перепишем наше равенство, переместив все в левую часть:
1) Предположим, что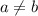
(при этом подразумевая, что 
)
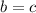Тогда получаем следующее:
Далее смотрим: слева неотрицательное выражение всегда, а справа может быть и отрицательное, но у нас по условию дано, что для любых действительных чисел равенство выполняется, а здесь это далеко не так (на языке математики запись такая: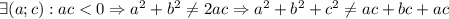
)
Возможно, это не очень явно, поэтому вспомним, что по предположению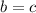
, и доделаем:
А это прямо яркий пример противоречия: предположив, что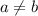
, мы получили 
.
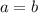Из этого следует, что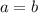
, но и из предположенного же 
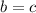уже следует, что 
.
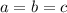Вообще, по идее, этого уже достаточно, ну на всякий случай посмотрим ещё:
2) Предположим, что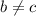
(при этом 
)
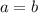И тогда уже точно исходя из пунктов 1) и 2), получаем