Белый медведь - самое крупное на
земле хищное млекопитающее. найди-
те значение выражения и вы узнаете о
белом медведе следующее:
1) (1 1/5 + 2,8 )*10в квадрате- от стольких кило-
граммов (400 *50 +5 * 8000) : 10вквадрате - до
стольких килограммов составляет
средняя масса белого медведя;
2) 3 (2вкубе*5вквадрате +10вквадрате) — столько килограммов
составляет масса самого большого
белого медведя; 3) 1/2(2 5/7+4 2/7)-столько метров составляет длина самого большого белого медведя​

Как известно, число подмножеств множества, состоящего из N элементов, равно (это если учитывать пустое множество и само множество). Доказать это можно с метода математической индукции. Формула очевидна для маленьких N. Например, если в множестве один элемент, то подмножеств два - пустое и само множество. Пусть для N-элементного множества число подмножеств равно Добавим еще один элемент. Все подмножества нового множества разбиваются на две категории - те, которые не содержат новый элемент (их по предположению

штук) и те, которые его содержат (их тоже

штук, так как они могут быть получены из подмножеств первого типа добавлением нового элемента). Всего получаем

подмножеств, что и требовалось доказать.

В нашем случае нужно подсчитать количество элементов множества. Это 3, 4, 5 и 6 (два в квадрате меньше шести, семь в квадрате больше 39), всего 4 числа. Остается найти число

Найти по одному решению каждого уравнения - не проблема. А вот найти все натуральные решения - это намного более сложная задача.

Простейшие решения в первой задаче (1;1)), во второй (3;2), в третьей (1;1). Дальше можете не смотреть (а можете посмотреть).

1) Преобразуем так: (x²-1)(y²-1)=0; x²-1=0 или y²-1=0; x=1 или y=1.

То есть решения такие: (1;1), (1;2), (1;3), ..., (2;1), (3;1),...

2) Преобразуем так: x²-2y²=1. Это намного более сложная задача - частный случай так называемого уравнения Пелля. Заинтересуетесь - почитайте литературу на эту тему, только сначала попробуйте решить сами. Годится, как я уже писал, пара (3;2), остальные пары получаются из этой по такому правилу: если была пара (x;y), то следующая равна (3x+4y;2x+3y). Поэтому получаем второе решение (3·3+4·2;2·3+3·2)=(17;12). Можете построить сколько угодно решений по такому правилу.

3) Конечно, если m=n, то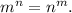 Поэтому мы уже имеем бесконечное множество решений. Но ими множество решений не исчерпывается. По крайней мере 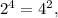то есть получили решения (2;4) и (4;2). Докажем, что других решений нет. Преобразуем так:

Рассмотрим функцию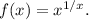 (x≥1)

Слева от e производная положительна, справа отрицательна, то есть слева от e функция возрастает, справа убывает.

при этом все эти числа  кроме f(1) больше 1. Поэтому кроме f(2)=f(4) все эти числа разные.

ответ в третьей задаче: (2;4), (4;2), (1;1), (2;2), (3;3),...

прощения, если не все было понятно - в будущем разберетесь))