Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Х
Химия
Д
Другие предметы
Н
Немецкий язык
Б
Беларуская мова
М
Музыка
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
У
Українська література
Р
Русский язык
Ф
Французский язык
П
Психология
О
Обществознание
А
Алгебра
М
МХК
Г
География
И
Информатика
П
Право
А
Английский язык
Г
Геометрия
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
enrnud6
09.01.2022 00:20 •
Алгебра
дам 20б.
Решить уравнение используя снижения порядка
x(y''+1)+y'=0
Показать ответ
Ответ:
LONNI34
11.10.2020 20:45
Понизим порядок с замены
, тогда
Выполним обратную замену
0,0
(0 оценок)
Популярные вопросы: Алгебра
Katyha028272819
05.01.2023 22:16
за кожну відповідність 0, установити відповідність між випробуванням (1-4) та ймовірністю(A-Г)...
lord50
23.03.2022 11:09
Скільки різних п ятицифрових чисел можна записати використовуючи в запису хоча б одну цифру 0...
ernis024
13.02.2022 03:02
На картках записано числа від 1 до 12. Навмання беруть дві з них. Яка ймовірність того, що сума чисел на картках дорівиюе 12?...
Nastya7654321
15.07.2021 09:06
Выразив переменную y через переменную x, найдите два каких-либо решения уравнения:1) 1,4x+y=22) x-5y-3=03) 2x+7y=10...
Lera246hh
12.06.2020 04:41
Представьте число в виде произведения степеней простых чисел: а) 18×20×22 б) 243×15×125....
Артём244
12.06.2020 04:41
Какому из указанных промежутков принадлежат корни √25-√x² +√9-√x²=9x^4 +8...
nasty301
01.06.2020 14:38
Вставьте вместо многоточия верные выражения, чтобы получилось равенство, используй ФСУ 1-задание1) 0.027x^3+1=...+1=(…+1)(…-...+1); 2) x^3+8y^3 z^9=(x+...)(x^2-...+...);3) 8x^3+y^6=(…+y^2...
VAI81416
23.09.2021 03:35
Напиши вариант ответа...
1ТекуОтОтветов
03.03.2020 07:52
Выберите правельный вариант ответов. ...
Всеникизаняты00
05.12.2020 17:28
Упростите 1) 15(8х-1)-8(15х+4) 2) 5b(3a-b)-3a(5b+a) 3) a(-3n)-n(+a)...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Понизим порядок с замены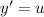 , тогда
, тогда 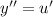
Выполним обратную замену