Х²+8х+18=х²+2*4х+4²+2=(х+4)²+2 Квадрат числа - это либо положительное число, либо ноль. То есть (х+4)²≥0. Если к положительному числу или нулю добавить 2, то получится положительное число. Значит, выражение принимает положительное значение при любом значении х. Наименьшее значение выражение примет в том случае, если значение выражения (х+4)² будет наименьшим, то есть 0, поскольку квадрат числа не может быть отрицательным. При этом значение выражения будет равно 0+2=2. Итак, найдем х, при котором выражение принимает наименьшее значение: (х+4)²=0 х+4=0 х=0-4 х=-4 - при таком значении х значение будет наименьшим. ответ: наименьшее значение выражения будет 2 при х=-4.
Если одно из чисел (n или n-1) не делится ни на 2, ни на 5, то оно взаимно просто с 10000, и другое число обязано делиться на 10000. Очевидно, таких четырехзначных n, что n или n-1 делится на 10000, нет. Значит, оба числа делятся на 2 или на 5. Два числа вместе делиться на 2 или на 5 не могут, т.к. различаются на 1. Значит, одно из них делится на 2 (не делится на 5), а другое на 5 (не делится на 2).
Пусть, n = * b (a - степень вхождения 5 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 5, поэтому, чтобы n(n-1) делилось на , нужно чтобы а было ≥ 4.
n ≡ 0 mod .
Аналогично n-1 ≡ 0 mod (т.к. n не делится на 2) ⇒ n ≡ 1 mod 2^4
Видно, что n = 625 подходит. По кит. т. об остатках, все остальные n получаются прибавлением константы * = 10000, умноженной на целое число. Значит, таких четырехзначных n не существует.
Пусть, n = * b (a - степень вхождения 2 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 2, поэтому, чтобы n(n-1) делилось на , нужно чтобы а было ≥ 4.
n ≡ 0 mod
Аналогично n-1 ≡ 0 mod (т.к. n не делится на 5) ⇒ n ≡ 1 mod 5^4
Видно, что n = 9376 подходит. По кит. т. об остатках, все остальные n получаются прибавлением константы * = 10000, умноженной на целое число. Значит, существует только 1 четырехзначное n = 9376.
Квадрат числа - это либо положительное число, либо ноль. То есть (х+4)²≥0. Если к положительному числу или нулю добавить 2, то получится положительное число. Значит, выражение принимает положительное значение при любом значении х.
Наименьшее значение выражение примет в том случае, если значение выражения (х+4)² будет наименьшим, то есть 0, поскольку квадрат числа не может быть отрицательным. При этом значение выражения будет равно 0+2=2.
Итак, найдем х, при котором выражение принимает наименьшее значение:
(х+4)²=0
х+4=0
х=0-4
х=-4 - при таком значении х значение будет наименьшим.
ответ: наименьшее значение выражения будет 2 при х=-4.
Одно: n = 9376
Объяснение:
n(n-1) делится на 10^4.
Если одно из чисел (n или n-1) не делится ни на 2, ни на 5, то оно взаимно просто с 10000, и другое число обязано делиться на 10000. Очевидно, таких четырехзначных n, что n или n-1 делится на 10000, нет. Значит, оба числа делятся на 2 или на 5. Два числа вместе делиться на 2 или на 5 не могут, т.к. различаются на 1. Значит, одно из них делится на 2 (не делится на 5), а другое на 5 (не делится на 2).
Пусть, n =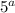 * b (a - степень вхождения 5 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 5, поэтому, чтобы n(n-1) делилось на
* b (a - степень вхождения 5 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 5, поэтому, чтобы n(n-1) делилось на 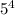 , нужно чтобы а было ≥ 4.
, нужно чтобы а было ≥ 4.
n ≡ 0 mod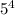 .
.
Аналогично n-1 ≡ 0 mod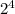 (т.к. n не делится на 2) ⇒ n ≡ 1 mod 2^4
(т.к. n не делится на 2) ⇒ n ≡ 1 mod 2^4
Видно, что n = 625 подходит. По кит. т. об остатках, все остальные n получаются прибавлением константы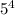 *
* 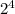 = 10000, умноженной на целое число. Значит, таких четырехзначных n не существует.
= 10000, умноженной на целое число. Значит, таких четырехзначных n не существует.
Пусть, n =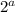 * b (a - степень вхождения 2 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 2, поэтому, чтобы n(n-1) делилось на
* b (a - степень вхождения 2 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 2, поэтому, чтобы n(n-1) делилось на 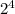 , нужно чтобы а было ≥ 4.
, нужно чтобы а было ≥ 4.
n ≡ 0 mod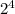
Аналогично n-1 ≡ 0 mod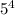 (т.к. n не делится на 5) ⇒ n ≡ 1 mod 5^4
(т.к. n не делится на 5) ⇒ n ≡ 1 mod 5^4
Видно, что n = 9376 подходит. По кит. т. об остатках, все остальные n получаются прибавлением константы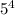 *
* 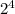 = 10000, умноженной на целое число. Значит, существует только 1 четырехзначное n = 9376.
= 10000, умноженной на целое число. Значит, существует только 1 четырехзначное n = 9376.
Если моё решение Вам отметьте его как лучшее.