Умножим левую и правую части неравенства на и умножим отдельные множители на каждую скобку.
Это верно для всех х, кроме х = πn/2, n ∈ Z
Умножим левую и правую части неравенства на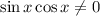 и умножим отдельные множители на каждую скобку.
и умножим отдельные множители на каждую скобку.
Это верно для всех х, кроме х = πn/2, n ∈ Z