от e^x производная e^x, а у тя сложная функция, т.е надо еще найти производную от 1/(2-x) и умножить на нее.
от e^x производная e^x, а у тя сложная функция, т.е надо еще найти производную от 1/(2-x) и умножить на нее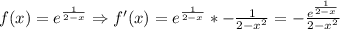 .
.