Совокупность всех первообразных функции называют неопределенным интегралом:
где — произвольная постоянная.
Тогда
Теорема: если функции и являются соответственно первообразными функций и на промежутке , то на этом промежутке функция является первообразной функции
где — произвольная постоянная.
Тогда
Теорема: если функция является первообразной для функции на промежутке , а — некоторое число, то на этом промежутке функция является первообразной функции
Тогда
Теорема: если функция является первообразной для функции на промежутке , а — некоторое число, отличное от нуля, то на соответствующем промежутке функция является первообразной функции
где — произвольная постоянная.
Найдем каждый интеграл по отдельности:
Получаем:
Таким образом, общий вид первообразных для функции имеет вид:
‥・Здравствуйте, tydlidas2007! ・‥
• Шаг за шагом объяснение:
Для того, чтобы нам решить данную задачу, то мы должны сначала записать задачу в виде чисел:
• Задача в виде слов: Минус три умножить на минус одна треть.
Минус три: -3;
Умножить: ×;
Минус одна треть: -1/3.
• Задача в виде чисел: -3×-1/3.
А теперь, после того, как мы записали данную задачу в виде чисел, то мы можем делать следующее:
• 1. Произведение двух отрицательных значений положительно: (-)×(-)=(+), то есть, вычислить: 3×1/3.
• 2. Сократить числа на наибольший общий делитель 3, то есть, сократить дробь: 1.
У нас в ответе получается число 1, значит, минус три умножить на минус одна треть равно (получается) один. (-3×(-1/3)=1)
‥・С уважением, Ваша GraceMiller! :) ・‥
Совокупность всех первообразных функции называют неопределенным интегралом:
называют неопределенным интегралом:
где — произвольная постоянная.
— произвольная постоянная.
Тогда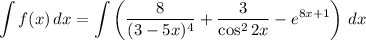
Теорема: если функции и
и 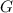 являются соответственно первообразными функций
являются соответственно первообразными функций 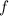 и
и 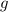 на промежутке
на промежутке 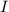 , то на этом промежутке функция
, то на этом промежутке функция  является первообразной функции
является первообразной функции 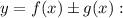
где — произвольная постоянная.
— произвольная постоянная.
Тогда
Теорема: если функция является первообразной для функции
является первообразной для функции 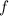 на промежутке
на промежутке 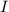 , а
, а  — некоторое число, то на этом промежутке функция
— некоторое число, то на этом промежутке функция  является первообразной функции
является первообразной функции 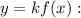
Тогда
Теорема: если функция является первообразной для функции
является первообразной для функции 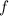 на промежутке
на промежутке 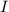 , а
, а  — некоторое число, отличное от нуля, то на соответствующем промежутке функция
— некоторое число, отличное от нуля, то на соответствующем промежутке функция 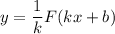 является первообразной функции
является первообразной функции 
где — произвольная постоянная.
— произвольная постоянная.
Найдем каждый интеграл по отдельности:
Получаем:
Таким образом, общий вид первообразных для функции имеет вид:
имеет вид:
ответ:
Использованные формулы интегрирования: