Исследование и построение графиков функции
y=-x² + 4x + 1

1. 1) Очевидно

2) Очевидно

3) Очевидно ибо под учеником подразумевается 12 девочек и 13 мальчиков, т.е. всего учеников 12 + 13 = 25.

4) К любой из 12 девочек в пару можно взять любого из 13 мальчиков. По правилу произведения всего существует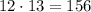 выбрать мальчика с девочкой.

ОТВЕТ: 1) 12; 2) 13; 3) 25; 4) 156.

2. Есть 10 цифр, из которых нужно составить четырехзначные числа.

1) Если цифры не могут повторяться, рассуждаем следующим образом. На первом месте может стоять любая из цифр, кроме 0, т.е. существует выбрать цифру, обозначающую тысячи. На втором месте может стоять любая из 9 оставшихся цифр, т.е. цифру, обозначающую сотни, также можно выбрать Аналогично цифру, обозначающую десятки, можно выбрать так как останется 8 цифр; цифру, обозначающую единицы

По правилу произведения всего можно составить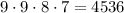 четырехзначных чисел.

2) Если цифры не могут повторяться, рассуждаем следующим образом. На первом месте может стоять любая из цифр, кроме 0 - имеем выбора первой цифры. Однако так как цифры могут повторяться, каждую следующую цифру числа можно выбрать

По правилу произведения всего можно составить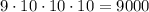 четырехзначных чисел.

ОТВЕТ: 1) 4536;  2)9000.

1)

y-2x=1

6x-y=7   y=6x-7

6x-7-2x=1

6x-2x=1+7

4x=8

x=8:4

x=2

y=6*2-7

y=5

2)

x+y=6   x=6-y

3x-5y=2

3(6-y)-5y=2

18-3y-5y=2

-8y=-16

y=-16:-8

y=2

x=6-2

x=4

3)

7x-3y=13

x-2y=5   x=5+2y

7(5+2y)-3y=13

35+14y-3y=13

11y=13-35

11y= -22

y=-22:11

y=-2

x=5+2*(-2)

x=9

4)

2x+y=12   y= 12-2x

7x-2y=31

7x-2(12-2x)=31

7x-24+4x=31

11x=31+24

11x=55

x=55:11

x=5

y=12-2*5

y=2

5)

4x-y=11   y=4x-11

6x-2y=13  

6x-2(4x-11)=13

6x-8x+22=13

-2x=13-22

-2x=-9

x=-9:-2

x=4,5

y=4*4,5-11

y=18-11

y=7

6)

8y-x=4   x=-4+8y

2x-21y=2

2(-4+8y)-21y=2

-8+16y-21y=2

-5y=2+8

-5y=10

y=10:-5

y=-2

x=-4+8*-2

x=-20

Объяснение: