Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
yaam13
10.09.2021 16:07 •
Алгебра
Извлеките квадратный корень, если m<0, n<0
решите , с пояснениями
Показать ответ
Ответ:
nikysha04
13.08.2021 17:34
Воспользуемся формулой
:
Модули
и
раскрывали со сменой знака, так как m и n - отрицательные числа.
0,0
(0 оценок)
Популярные вопросы: Алгебра
Татьяна72828
09.04.2021 06:32
Найди произведение многочлена и одночлена 2(8a2степень−7a+12). ответ: a2степень− a+ ....
Evazaur
10.09.2022 03:53
C) 5х + 9 = 17; d) 132х4 b) 23х + 5 =-7; c) 23х –7 = 21; | d) 16х+33Пока:ПокаВходП2щиеУпражненияРешите уравнение (10—19):b) 4х – 6 = 9;10. а) 3х + 5 =-8 ;11.а) (12x –...
Makc920
09.05.2021 17:50
Найдите значение выражения -0,9^2...
aushatsy
31.08.2020 13:30
80,25^2-79,75^2/0,4^2+1,28+1,6^2...
Lilu700
30.08.2022 03:38
Sin(84°-a)cos(a+24°)-cos(84°-a)sin(a+24)...
Kam54
11.12.2022 18:20
Найдите производную функции ()=(∛2+4)...
HappyGamerAND3000
08.05.2020 14:51
алгкбр 7 клааасс проверочная...
nik868
02.09.2022 03:30
Таблица 7.6 равнобедренный треугольник 9)...
Режик
18.02.2020 05:59
Преобразуйте выражение так, чтобы оно не содержало степеней с отрицательным показателем: (3/5×a^-8×b^-7)^6×(-5а^6×b^12)^-2...
Wonderfulgirl30
30.12.2020 12:21
Sin5x-sin3x=2решите уравнение ...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Воспользуемся формулой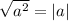 :
:
Модули и
и  раскрывали со сменой знака, так как m и n - отрицательные числа.
раскрывали со сменой знака, так как m и n - отрицательные числа.