На координатной плоскости построены игрек равно минус 2 минус 6 игрек равно минус х минус 5 Используя эти графики решите систему уравнений {у=-2х-6. {у=-х-5 ответ...
Решение подобного биквадратного уравнения сводится к замене вида:
Исходя из области определения корнями будут:
ответ:
Область определения уравнения:
Преобразовывая область определения отбросим левую часть,так как корень равен неотрицательному числу(в данном случае числом является x,и при отрицательных x равенство не имеет место)
Возведем обе неотрицательные части в четвертую степень:
Решение подобного биквадратного уравнения сводится к замене вида:
Пусть у Миши было х рублей, тогда у Коли было 28-х рублей.
Миша потратил 75%, после чего у него осталось 100%-75%=25% или 1/4 часть денег, т.е. х/4 руб.
Коля потратил 2/3 своих денег, после чего у него осталось 1-2/3=1/3 часть денег, т.е. (28-х)/3 руб.
По условию задачи, денег у мальчиков стало поровну. Составляем уравнение:
х/4 = (28-х)/3 |*12
3x=(28-x)*4
3x=28*4-4x
3x+4x=112
7x=112
x=16(руб.)-было у Миши
28-х=28-16=12(руб.)-было у Коли
Проверка: 16+12=28
ответ: У Миши было 16 рублей, а у Коли было 12 рублей.
1)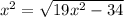
Область определения уравнения:
Возведем обе неотрицательные части в квадрат:
Решение подобного биквадратного уравнения сводится к замене вида: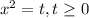
Исходя из области определения корнями будут:
ответ: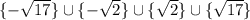
Область определения уравнения:
Преобразовывая область определения отбросим левую часть,так как корень равен неотрицательному числу(в данном случае числом является x,и при отрицательных x равенство не имеет место)
Возведем обе неотрицательные части в четвертую степень:
Решение подобного биквадратного уравнения сводится к замене вида: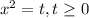
Исходя из области определения корнями будут:
ответ: