√61
Объяснение:
Найдём производную относительно x (то есть представим выражение как функцию z с параметром y):
Аналогично найдём производную относительно y:
Найдём точки экстремума. Для этого обе производные должны быть одновременно равны нулю:
Выразим y² из первого уравнения:
Левая часть положительна (нулём быть не может, так как она была в знаменателе), значит, и правая часть положительна:
Выразим x² из второго уравнения (уравнения практически одинаковые, поэтому некоторые преобразования я опущу):
Подставим :
Так как 0 < x < 3, в данном случае корней нет.
Так как 0 < x < 3, подходит только один корень .
— удовлетворяет условию 0 < y < 3.
— точка экстремума.
Исследуем знаки производной относительно x при . При , например, при , производная имеет знак:
Производная имеет знак минус. При , например, при x = 1, производная имеет знак:
Производная имеет знак плюс. Значит, — точка минимума.
Аналогично исследуем знаки производной относительно y при . При , например, при , производная имеет знак:
Производная имеет знак минус. При , например, при y = 1, производная имеет знак:
Значит, — точка минимума всей функции. Значение выражения в данной точке равно:
√61
Объяснение:
Найдём производную относительно x (то есть представим выражение как функцию z с параметром y):
Аналогично найдём производную относительно y:
Найдём точки экстремума. Для этого обе производные должны быть одновременно равны нулю:
Выразим y² из первого уравнения:
Левая часть положительна (нулём быть не может, так как она была в знаменателе), значит, и правая часть положительна:
Выразим x² из второго уравнения (уравнения практически одинаковые, поэтому некоторые преобразования я опущу):
Подставим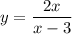 :
:
Так как 0 < x < 3, в данном случае корней нет.
Подставим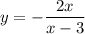 :
:
Так как 0 < x < 3, подходит только один корень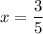 .
.
Исследуем знаки производной относительно x при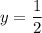 . При
. При 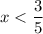 , например, при
, например, при 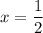 , производная имеет знак:
, производная имеет знак:
Производная имеет знак минус. При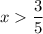 , например, при x = 1, производная имеет знак:
, например, при x = 1, производная имеет знак:
Производная имеет знак плюс. Значит,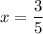 — точка минимума.
— точка минимума.
Аналогично исследуем знаки производной относительно y при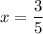 . При
. При 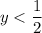 , например, при
, например, при 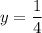 , производная имеет знак:
, производная имеет знак:
Производная имеет знак минус. При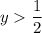 , например, при y = 1, производная имеет знак:
, например, при y = 1, производная имеет знак:
Производная имеет знак плюс. Значит,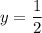 — точка минимума.
— точка минимума.
Значит,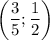 — точка минимума всей функции. Значение выражения в данной точке равно:
— точка минимума всей функции. Значение выражения в данной точке равно: