Смотри. У тебя дано расстояние равное 52,2. Дано время движения против течения и по течению. 4,5 и 2,1 часа соответственно. Скорость течения реки тоже известна, 3 км.ч. Следовательно скорость катера по течению будет равна x+3км.ч. А против течения x-3км.ч. Где икс - собственная скорость катера. Составляем уравнение. 52,2=(x+3)*2,1=(x-3)*4,5. Получаем. (x+3)*2,1-(x-3)*4,5=0. 2,1x+6,3-4,5x+13,5=0. Числа в одну сторону, иксы в другую. 2.1x-4,5x=-6,3-13,5 -2,4x=-19.8 x=8,25 км.ч(когда делишь отрицательное число на отрицательное, получаешь положительное) ответ: Скорость катера равна 8,25 км.ч
Дано время движения против течения и по течению. 4,5 и 2,1 часа соответственно.
Скорость течения реки тоже известна, 3 км.ч.
Следовательно скорость катера по течению будет равна x+3км.ч.
А против течения x-3км.ч.
Где икс - собственная скорость катера.
Составляем уравнение.
52,2=(x+3)*2,1=(x-3)*4,5.
Получаем.
(x+3)*2,1-(x-3)*4,5=0.
2,1x+6,3-4,5x+13,5=0.
Числа в одну сторону, иксы в другую.
2.1x-4,5x=-6,3-13,5
-2,4x=-19.8
x=8,25 км.ч(когда делишь отрицательное число на отрицательное, получаешь положительное)
ответ: Скорость катера равна 8,25 км.ч
а) две точки пересечения (два корня)
b)
Объяснение:
a)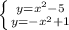
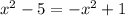в) 
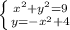окружность R=3, O(0;0) и
б) xy=3 или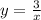
гипербола, точка симметрии (0;0)
точек пересечения графиков нет, самые близкие точки к началу кординат в точках х=у, у гиперболы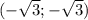
и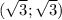 
у окружност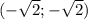и
и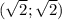 
г)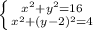
это две окружности: одна R=4, центр (0;0)
другая R=2 центр (0;2), точка касания (0;4) одна.
ну а графики придется рисовать по клеткам, используя циркуль и лекала для точности построения. Удачи.