Чтобы решить графически уравнение, нужно построить два графика: для функции слева и функции справа от знака равенства.
1) - степенная функция с отрицательным показателем (-3) называется гиперболой третьего порядка. Ветви параболы расположены в первой и третьей четвертях (k=8 > 0)
Область определения x≠0 ⇒ x ∈ (-∞; 0) ∪ (0; +∞)
Область значений функции y ∈ (-∞; 0) ∪ (0; +∞)
Точки для построения
x : 1 -1 2 -2 4 -4
y : 8 -8 1 -1 1/8 -1/8
2) y = (x + 1)³ - степенная функция с натуральным показателем. График - кубическая парабола.
Область определения x ∈ R
Область значений функции y ∈ R
Точки для построения
x : 0 1 -1 2 -2 -3
y : 1 8 0 27 -1 -8
Графики представлены в приложении.
Графики пересекаются в двух точках А(1; 8) и B(-2; -1). Координаты х точек пересечения являются решением уравнения .
Чтобы решить графически уравнение, нужно построить два графика: для функции слева и функции справа от знака равенства.
1)
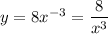- степенная функция с отрицательным показателем (-3) называется гиперболой третьего порядка. Ветви параболы расположены в первой и третьей четвертях (k=8 > 0)
Область определения x≠0 ⇒ x ∈ (-∞; 0) ∪ (0; +∞)
Область значений функции y ∈ (-∞; 0) ∪ (0; +∞)
Точки для построения
x : 1 -1 2 -2 4 -4
y : 8 -8 1 -1 1/8 -1/8
2) y = (x + 1)³ - степенная функция с натуральным показателем. График - кубическая парабола.
Область определения x ∈ R
Область значений функции y ∈ R
Точки для построения
x : 0 1 -1 2 -2 -3
y : 1 8 0 27 -1 -8
Графики представлены в приложении.
Графики пересекаются в двух точках А(1; 8) и B(-2; -1). Координаты х точек пересечения являются решением уравнения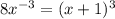
.
ответ : x₁ = 1; x₂ = -2