Определим общее число расстановок на пяти позициях 5 шариков:
Однако, среди этих расстановок есть недопустимые (то есть те, при которых между зеленым и желтым шариком располагаются два или более шарика). Найдем число недопустимых расстановок.
Найдем число недопустимых размещений зеленого и желтого шарика. Их можно просто перечислить:
1) зеленый на 1-ом месте, желтый на 4-ом месте
2) зеленый на 1-ом месте, желтый на 5-ом месте
3) зеленый на 2-ом месте, желтый на 5-ом месте
4) зеленый на 4-ом месте, желтый на 1-ом месте
5) зеленый на 5-ом месте, желтый на 1-ом месте
6) зеленый на 5-ом месте, желтый на 1-ом месте
В каждом из этих случаев оставшиеся три шарика могут размещаться на свободных местах
Таким образом, всего имеется недопустимых расстановок.
По условию задачи, если к некоторому палиндрому (х+3) прибавить 2, то получится также палиндром (х+5). Найдем этот палиндром (х+3).
Заметим, что если при прибавлении к числу 2 не произошло перехода в старшие разряды, то получившееся число не будет палиндромом. Значит, последняя цифра числа (х+3) равна 8 или 9. Тогда, после прибавления к такому числу 2, его последняя цифра станет равной 0 или 1 соответственно. Но по смыслу палиндрома, эта же цифра должна являться и его первой цифрой. Единственный возможный вариант - произошел переход через все разряды вплоть до старшего в исходном числе.
Единственное число-палиндром, при прибавлении к которому 2 произойдет переход по всем разрядам - это число 9999. Заметим, что результат суммы 9999+2=10001 - палиндром.
Определим общее число расстановок на пяти позициях 5 шариков:
Однако, среди этих расстановок есть недопустимые (то есть те, при которых между зеленым и желтым шариком располагаются два или более шарика). Найдем число недопустимых расстановок.
Найдем число недопустимых размещений зеленого и желтого шарика. Их можно просто перечислить:
1) зеленый на 1-ом месте, желтый на 4-ом месте
2) зеленый на 1-ом месте, желтый на 5-ом месте
3) зеленый на 2-ом месте, желтый на 5-ом месте
4) зеленый на 4-ом месте, желтый на 1-ом месте
5) зеленый на 5-ом месте, желтый на 1-ом месте
6) зеленый на 5-ом месте, желтый на 1-ом месте
В каждом из этих случаев оставшиеся три шарика могут размещаться на свободных местах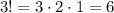
Таким образом, всего имеется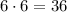
недопустимых расстановок.
Значит, допустимых расстановок имеется:
ответ: 84
По условию задачи, если к некоторому палиндрому (х+3) прибавить 2, то получится также палиндром (х+5). Найдем этот палиндром (х+3).
Заметим, что если при прибавлении к числу 2 не произошло перехода в старшие разряды, то получившееся число не будет палиндромом. Значит, последняя цифра числа (х+3) равна 8 или 9. Тогда, после прибавления к такому числу 2, его последняя цифра станет равной 0 или 1 соответственно. Но по смыслу палиндрома, эта же цифра должна являться и его первой цифрой. Единственный возможный вариант - произошел переход через все разряды вплоть до старшего в исходном числе.
Единственное число-палиндром, при прибавлении к которому 2 произойдет переход по всем разрядам - это число 9999. Заметим, что результат суммы 9999+2=10001 - палиндром.
Таким образом, число (х+3) найдено и равно 9999.
Значит, х=9996.
ответ: 9996