Пусть точка C(0, m) - центр окружности (так как по условию центр лежит на оси OY, то первая координата равна 0)
Известно, что расстояние от центра до любой точки на окружности является константой и равно радиусу R окружности
Наша окружность проходит через точку 7 на оси OY, значит R = 7 - m
Также окружность проходит через точку 5 на оси OX, значит по теореме Пифагора
Приравняем это и получим уравнение:
Возвёдём в квадрат и решим уравнение:
Координата центра окружности -
Радиус окружности:
Уравнение окружности выглядит следующим:
Подставим наши числа:
ответ:
Пусть точка C(0, m) - центр окружности (так как по условию центр лежит на оси OY, то первая координата равна 0)
Известно, что расстояние от центра до любой точки на окружности является константой и равно радиусу R окружности
Наша окружность проходит через точку 7 на оси OY, значит R = 7 - m
Также окружность проходит через точку 5 на оси OX, значит по теореме Пифагора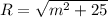
Приравняем это и получим уравнение:
Возвёдём в квадрат и решим уравнение:
Координата центра окружности -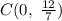
Радиус окружности: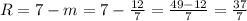
Уравнение окружности выглядит следующим:
Подставим наши числа:
ответ: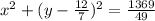
х;у;z;...-члены прогрессии
х; у+8;z;... - арифметическая прогрессия
х;у+1;z+11 ...-геометр.прогрессия
{y^2=xz; y^2=xz; y^2=xz; y^2=x(2y-x+16)
{y+8=(x+z)/2; 2y+16=x+z; z=2y-x+16 z=2y-x+16
{(y+1)^2=x(z+11); y^2+2y+1-xz-11x=0; y^2+2y+1-y^2-11x=0; 2y-11x+1=0
Решаем {y^2=x(2y-x+16); ((11x-1)^2)/4 -x(11x-1-x+16)=0
{2y-11x+1=0; y=(11x-1)/2
121x^2-22x+1-4x(10x+15)=0
121x^2-22x+1-40x^2-60x=0
81X^2- 82x+1=0
D1=41^2-81*1=1681-81=1600=40^2
x1=(41-40)/81=1/81; x2=(41+40)/81=1
x=1; y=(11*1-1)/2=5; z=2*5-1+16=25
x=1/81; y=1/81-1=-80/81; z=-160/81-1/81+16=1135/81-не является геом. прогрессией(может ошибка где? Проверьте
ответ. 1;5;25
;