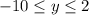Запишем формулу: P=m/n, где m – число исходов, благоприятствующих осуществлению события X, а n – число всех равновозможных элементарных исходов.
Для начала определим вероятность выпадения какого-либо числа при одном броске. Определённое число выпадает одно, а всего исходов может быть 6 (6 граней кубика). Значит, вероятность выпадения какого-либо числа = 1/6.
Так как бросков мы делаем 2, количество возможных результатов возводится во 2-ю степень, и вероятность выпадения какого-либо числа уже = 1 / 6 × 6 = 1/36. В последующем, мы будем домножать числитель на количество удовлетворяющих нас результатов.
Сумма выпавших очков делится на 5 при следующих результатах
1) 1 и 4 (=5)
2) 2 и 3 (=5)
3) 3 и 2 (=5)
4) 4 и 1 (=5)
5) 5 и 5 (=10)
Как видим, количество удовлетворяющих нас результатов = 5. Значит, вероятность выпадения числа, кратного 5 = 1 × 5 / 36 = 5/36 ≈ 0.139 = 13.9%
Сумма выпавших очков меньше, чем 8 при следующих результатах:
1) 1 и 1
2) 1 и 2
3) 1 и 3
4) 1 и 4
5) 1 и 5
6) 1 и 6
7) 2 и 1
8) 2 и 2
9) 2 и 3
10) 2 и 4
11) 2 и 5
12) 3 и 1
13) 3 и 2
14) 3 и 3
15) 3 и 4
16) 4 и 1
17) 4 и 2
18) 4 и 3
19) 5 и 1
20) 5 и 2
21) 6 и 1
Как видим, количество удовлетворяющих нас результатов = 21. Значит, вероятность выпадения чисел, сумма которых меньше 8 = 1 × 21 / 36 = 21/36 = 7/12 ≈ 0.583 = 58.3%
Произведение выпавших очков делится на 12 при следующих результатах:
1) 2 и 6
2) 3 и 4
3) 4 и 3
4) 6 и 2
Как видим, количество удовлетворяющих нас значений =4. Значит, вероятность выпадения чисел, произведение которых =12 составляет 1 × 4 / 36 = 4/36 = 1/9 ≈ 0,111 = 11,1%
Количество очков, выпавших в первый раз, и количество очков, выпавших
во второй раз, отличаются на 3 возможно при следующих результатах:
1) 1 и 4
2) 4 и 1
3) 2 и 5
4) 5 и 2
5) 3 и 6
6) 6 и 3
Как видим, количество удовлетворяющих нас результатов =6. Значит, вероятность выпадения чисел, количество очков которых, выпавших в первый раз, и количество очков, выпавших во второй раз, отличаются на 3 составляет 1 × 6 / 36 = 6/36 = 1/6 ≈ 0,166 = 16,6%
Запишем формулу: P=m/n, где m – число исходов, благоприятствующих осуществлению события X, а n – число всех равновозможных элементарных исходов.
Для начала определим вероятность выпадения какого-либо числа при одном броске. Определённое число выпадает одно, а всего исходов может быть 6 (6 граней кубика). Значит, вероятность выпадения какого-либо числа = 1/6.
Так как бросков мы делаем 2, количество возможных результатов возводится во 2-ю степень, и вероятность выпадения какого-либо числа уже = 1 / 6 × 6 = 1/36. В последующем, мы будем домножать числитель на количество удовлетворяющих нас результатов.
Сумма выпавших очков делится на 5 при следующих результатах
1) 1 и 4 (=5)
2) 2 и 3 (=5)
3) 3 и 2 (=5)
4) 4 и 1 (=5)
5) 5 и 5 (=10)
Как видим, количество удовлетворяющих нас результатов = 5. Значит, вероятность выпадения числа, кратного 5 = 1 × 5 / 36 = 5/36 ≈ 0.139 = 13.9%
Сумма выпавших очков меньше, чем 8 при следующих результатах:
1) 1 и 1
2) 1 и 2
3) 1 и 3
4) 1 и 4
5) 1 и 5
6) 1 и 6
7) 2 и 1
8) 2 и 2
9) 2 и 3
10) 2 и 4
11) 2 и 5
12) 3 и 1
13) 3 и 2
14) 3 и 3
15) 3 и 4
16) 4 и 1
17) 4 и 2
18) 4 и 3
19) 5 и 1
20) 5 и 2
21) 6 и 1
Как видим, количество удовлетворяющих нас результатов = 21. Значит, вероятность выпадения чисел, сумма которых меньше 8 = 1 × 21 / 36 = 21/36 = 7/12 ≈ 0.583 = 58.3%
Произведение выпавших очков делится на 12 при следующих результатах:
1) 2 и 6
2) 3 и 4
3) 4 и 3
4) 6 и 2
Как видим, количество удовлетворяющих нас значений =4. Значит, вероятность выпадения чисел, произведение которых =12 составляет 1 × 4 / 36 = 4/36 = 1/9 ≈ 0,111 = 11,1%
Количество очков, выпавших в первый раз, и количество очков, выпавших
во второй раз, отличаются на 3 возможно при следующих результатах:
1) 1 и 4
2) 4 и 1
3) 2 и 5
4) 5 и 2
5) 3 и 6
6) 6 и 3
Как видим, количество удовлетворяющих нас результатов =6. Значит, вероятность выпадения чисел, количество очков которых, выпавших в первый раз, и количество очков, выпавших во второй раз, отличаются на 3 составляет 1 × 6 / 36 = 6/36 = 1/6 ≈ 0,166 = 16,6%
ответ: 1) 13.9%; 2) 58.3%; 3) 11,1%; 4) 16,6%.
Объяснение:
1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.
В примере в) коэффициенты k=5, значит их графики параллельны.
2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.
3. АБВГ
2413
4. 2x + y = 8
2x - y = 1
Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:
2x - (8 - 2x) = 1
2x - 8 + 2x = 1
4x = 9
x = 2,25
y = 8 - 2*2,25 = 8 - 4,5 = 3,5
ответ: (2,25; 3,5)
5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.
2)
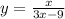. Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
б)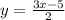
при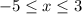 
Если x = -5, то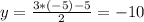
Если х= 3, то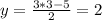
Значит,