Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Х
Химия
Д
Другие предметы
Н
Немецкий язык
Б
Беларуская мова
М
Музыка
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
У
Українська література
Р
Русский язык
Ф
Французский язык
П
Психология
О
Обществознание
А
Алгебра
М
МХК
Г
География
И
Информатика
П
Право
А
Английский язык
Г
Геометрия
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
1232508
13.09.2020 10:54 •
Алгебра
Sin^2(
+ x) = sinx + sin^2(
- x)
надеюсь у кого-то получится это решить.
Показать ответ
Ответ:
Аня276541
04.10.2020 19:32
0,0
(0 оценок)
Ответ:
Dhnsmvrxjns
04.10.2020 19:32
Объяснение:
Воспользуемся формулой понижения степени
Воспользуемся формулой
0,0
(0 оценок)
Популярные вопросы: Алгебра
castafirs
01.01.2020 02:13
Катер км по течению и 8 км по озеру затратив на весь путь 1 час скорость течения реки равна 3 км в час найдите скорость катера по течению...
2828371
01.01.2020 02:13
Графики функций y=-3x+2 и y=kx-5 пересекаются в некоторой точка a. найдите значение k при котором график функции y-kx+4 также проходит через точку а...
billymilligaan
19.02.2023 04:21
(1 целая 3/4+0,91)÷1,4+(1 целая 1/5-1,911)×1 целая 21/79 =?...
мистертомат
19.02.2023 04:21
Одна сторона треугольника вдвое больше второй,а третья на 5 см больше второй.вычислить стороны,если периметр 85 см...
p1pal1
19.02.2023 04:21
Принадлежит ли число —2 множеству чисел (сделайте запись с знаков ∈ и ∉ а) [ — 3; 0]; б) ( — 2; 3); в) (— ∞; —2]; г) ( — 2; + ∞]; д) n\ е) z; ж) q; з) r? и объясните...
чурка2829
19.02.2023 04:21
Доказать, пользуясь определением монотонных, функций, что функция: а) f(x) =x^2-3 (убывает) на промежутке (-бесконечность; 0] б) g(x) = 4x-3/x (дробь) (возростает)...
SoktoevTimur
07.03.2020 20:59
Aв квадрате - 9 разложите на множители...
юлия1384
16.07.2020 22:09
при якому значенні б значення виразів 3б+1 4б-1 б2+б б2+б+1 будуть послідовними числами...
yoruhoshi
03.03.2020 01:01
Найдите точки максимума и точки минимума функции y = 5-4x + 2x ^ 2x^2...
kabaramba
18.08.2022 14:00
Решить а) (c-x)² б)(с+4)² в)(5с-9х)² г)(6с+7)² д)(6-а)(6+а) е)(11у-4)(11у+4) ж)(2а-в)(4а²+2ав+в²) з)(7у+3х)(49у²-27ух+9х²)...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Объяснение:
Воспользуемся формулой понижения степени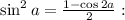
Воспользуемся формулой