Т.к. коэффициент при х² больше 0 (2 > 0), то ветви параболы направлены вверх => наименьшее значение функции совпадает со значением у в вершине параболы
Найдём координаты вершины параболы:
х = -(-1)/(2*2) = 1/4
у = 2*(1/4)² - 1/4 + а = 1/8 - 1/4 + а = -1/8 + а
Значит, (1/4; -1/8 + а) - вершина параболы
1) Наименьшее значение равно 2 => у вершины параболы равен 2 => -1/8 + а = 2 => а = 2 + 1/8 = 17/8
Значит, уравнение функции примет вид:
у = 2х² - х + 17/8
2) Наименьшее значение равно -4 => у вершины параболы равен -4 => -1/8 + а = -4 => а = -4 + 1/8 = -31/8
1)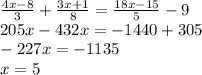
ответ: 5
ответ : x принадлежит R
2) ответ: нет решений, т.к. графики не пересекаются
3) Составим таблицу:
1 раствор 2 раствор смесь
концентрация 8 % 16% 11%
масса х мл у мл 400 мл
масса соли х*8/100 у*16/100 400*11/100
Тогда получим два уравнения
х+у=400
0,08х+0,16у=44
Решим полученную систему:
Вычтем из второго уравнения первое:
8x+16y-8x-8y=4400-3200
8y=1200
y=150 мл
Тогда х= 400-150=250 мл
ответ: Первого раствора 250 мл, второго 150 мл
у = 2х² - х + а - график функции парабола
Т.к. коэффициент при х² больше 0 (2 > 0), то ветви параболы направлены вверх => наименьшее значение функции совпадает со значением у в вершине параболы
Найдём координаты вершины параболы:
х = -(-1)/(2*2) = 1/4
у = 2*(1/4)² - 1/4 + а = 1/8 - 1/4 + а = -1/8 + а
Значит, (1/4; -1/8 + а) - вершина параболы
1) Наименьшее значение равно 2 => у вершины параболы равен 2 => -1/8 + а = 2 => а = 2 + 1/8 = 17/8
Значит, уравнение функции примет вид:
у = 2х² - х + 17/8
2) Наименьшее значение равно -4 => у вершины параболы равен -4 => -1/8 + а = -4 => а = -4 + 1/8 = -31/8
Значит, уравнение функции примет вид:
у = 2х² - х - 31/8
Графики смотри на фото