В равнобедренную трапецию вписана окружность найдите радиус окружности если длины оснований равны 4 и 16 см

Показать ответ

Ответ:

Medvedi47

01.01.2023 17:11

6)(x,y)=(-3/2,11/2)

Объяснение:

[x+y=11

[X- y=-7

Решим уравнение относительно y:

y+y=11

Приведём подобные члены:

2y =11|:2

[y=11/2

[X- y=-7

Подставим данное значение y в уравнение X- y=-7

x-11/2=-7

Перенесём постоянную в правую часть и сменим её знак :

x=-7+11/2

Вычислим сумму:

x=-3/2

Решением системы является упорядоченная пара чисел (x,y)=(-3/2 , 11/2)

Проверим , является ли упорядоченная пара чисел решением системы уравнений:

[11/2+11/2=11

[-3/2-11/2=-7

Упростим равенство:

[11=11

[-7=-7

Упорядоченная пара чисел является решением системы уравнений ,так как оба равенства верны.

(x,y)=(-3/2,11/2)

0,0(0 оценок)

Ответ:

sanyaleleckov

01.08.2020 22:11

Поскольку выражение под корнем должно быть неотрицательным, область определения - те иксы, при которых

$x^2-ax+9\geq 0$

Если это неравенство выполняется при всех , то областью определения функции будет любое число.

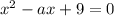Графиком функции в левой части является парабола, ветви которой направлены вверх. Парабола может пересечь ось не более чем в двух точках. Чтобы неравенство было верным для всех необходимо, чтобы эта парабола имела не более 1 точки пересечения с осью - т.е. либо одну, либо их вообще не должно быть. Ровно одна точка пересечения будет только в том случае, если уравнения x^2-ax+9=0 имеет одно решение (это возможно при 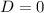D=0 ). Точек пересечения не будет вообще только в том случае, если уравнение 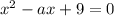не имеет решений (это возможно при 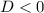). Оба условия нужно объединить: неравенство будет выполнено всегда, если $D\leq 0$ .